不等式＞0的解集是(1.2)．题目和参考答案——青夏教育精英家教网—

题目内容

18．不等式（x-1）（2-x）＞0的解集是（1，2）．

分析分析二次函数y=（x-1）（2-x）的图象和性质，可得不等式（x-1）（2-x）＞0的解集．

解答解：二次函数y=（x-1）（2-x）的图象是开口朝上，且与x轴交于点（1，0），（2，0），
故当1＜x＜2时，y=（x-1）（2-x）＞0，
故不等式（x-1）（2-x）＞0的解集是（1，2），
故答案为：（1，2）

点评本题考查的知识点是二次函数的性质，一元二次不等式的解法，熟练掌握三个二次之间的辩证关系，是解答的关键．

练习册系列答案

全国名师点拨小学毕业系统总复习系列答案

中考试题分类精华卷系列答案

第1卷单元月考期中期末系列答案

名校密卷小升初模拟试卷系列答案

相关题目

8．函数y=sin（x²）的图象大致是（　　）

9．与向量$\overrightarrow{a}$=（3，4，0）同向的单位向量$\overrightarrow{e}$=（$\frac{3}{5}$，$\frac{4}{5}$，0）．

6．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）离心率为$\frac{\sqrt{2}}{2}$，右焦点为F（c，0）到直线x=$\frac{{a}^{2}}{c}$的距离为1
（Ⅰ）求椭圆C的方程
（Ⅱ）不经过坐标原点O的直线l与椭圆C交于A，B两点，且线段AB中点在直线y=$\frac{1}{2}$x上，求△OAB面积的最大值．

13．关于x的不等式x²-ax-6a²＞0（a＜0）的解集为（-∞，x₁）∪（x₂，+∞），且x₂-x₁=5$\sqrt{2}$，则a的值为（　　）

-$\frac{\sqrt{5}}{2}$

3．在△ABC中，角A，B，C所对的边分别为a，b，c，且sin²B-sin²A=sin²C-sinAsinC．
（Ⅰ）求角B的值；
（Ⅱ）若△ABC的面积为$\sqrt{3}$，求a+c取得最小值时b的值．

10．直线l：y-1=k（x-1）和圆x²+y²-2x=0的位置关系是（　　）

7．

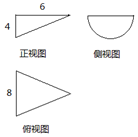某几何体的三视图是如图所示的直角三角形、半圆和等腰三角形，各边的长度如图所示，则此几何体的体积是16π，表面积是$24+（8+4\sqrt{13}）π$．

8．设直线l₁：kx-y+1=0，l₂：x-ky+1=0，若l₁∥l₂，则k=（　　）