题目内容
19.已知函数$f(x)=\left\{\begin{array}{l}{x^2}+2x-3,x≤0\\ lnx-a,x>0\end{array}\right.({a∈R})$,若关于x的方程f(x)=k有三个不相等的实数根,则实数k的取值范围是( )| A. | (-∞,-4) | B. | [-4,-3] | C. | (-4,-3] | D. | [-3,+∞) |
分析 作出函数$f(x)=\left\{\begin{array}{l}{x^2}+2x-3,x≤0\\ lnx-a,x>0\end{array}\right.({a∈R})$的图象,结合图象,能求出实数k的取值范围.
解答 解:作出函数$f(x)=\left\{\begin{array}{l}{x^2}+2x-3,x≤0\\ lnx-a,x>0\end{array}\right.({a∈R})$的图象,如下图: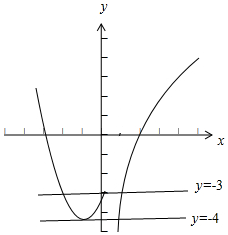
∵关于x的方程f(x)=k有三个不等的实根,
∴函数$f(x)=\left\{\begin{array}{l}{x^2}+2x-3,x≤0\\ lnx-a,x>0\end{array}\right.({a∈R})$的图象与直线y=k在三个不同的交点,
结合图象,得:-4<k≤-3.
∴实数k的取值范围是(-4,-3].
故选C.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
10.直线l:y-1=k(x-1)和圆x2+y2-2x=0的位置关系是( )
| A. | 相离 | B. | 相切或相交 | C. | 相交 | D. | 相切 |
8.设直线l1:kx-y+1=0,l2:x-ky+1=0,若l1∥l2,则k=( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 0 |
9.下列函数中,是偶函数且在区间(0,+∞)上是减函数( )
| A. | y=$\frac{1}{x}$ | B. | y=x2 | C. | y=($\frac{1}{2}$)x | D. | y=$\frac{1}{{x}^{2}}$ |
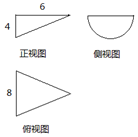 某几何体的三视图是如图所示的直角三角形、半圆和等腰三角形,各边的长度如图所示,则此几何体的体积是16π,表面积是$24+(8+4\sqrt{13})π$.
某几何体的三视图是如图所示的直角三角形、半圆和等腰三角形,各边的长度如图所示,则此几何体的体积是16π,表面积是$24+(8+4\sqrt{13})π$. 如图,在四棱锥中P-ABCD,AB=BC=CD=DA,∠BAD=60°,AQ=QD,△PAD是正三角形.
如图,在四棱锥中P-ABCD,AB=BC=CD=DA,∠BAD=60°,AQ=QD,△PAD是正三角形.