题目内容
给出下列命题:
①非零向量
,
满足|
+
|=|
-
|,则
,
的夹角为90°;
②
•
>0是向量
,
的夹角为锐角的充要条件;
③将函数y=sin(2x-
)的图象按向量
=(-
,0)平移,得到的图象对应的函数表达式为y=sin2x.
其中正确的命题编号是( )
①非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
②
| a |
| b |
| a |
| b |
③将函数y=sin(2x-
| π |
| 3 |
| a |
| π |
| 6 |
其中正确的命题编号是( )
| A、②③ | B、①② | C、①③ | D、①②③ |
考点:命题的真假判断与应用
专题:平面向量及应用,简易逻辑
分析:①由于非零向量
,
满足|
+
|=|
-
|,则
2+
2+2
•
=
2+
2-2
•
,可得
•
=0,即可得出;
②由于当<
,
>=0时也满足条件,因此表示充要条件;
③将函数y=sin(2x-
)的图象按向量
=(-
,0)平移,得到的y=sin[2(x+
)-
]=sin2x,即可得出.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
②由于当<
| a |
| b |
③将函数y=sin(2x-
| π |
| 3 |
| a |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
解答:
解:①非零向量
,
满足|
+
|=|
-
|,则
2+
2+2
•
=
2+
2-2
•
,可得
•
=0,因此
,
的夹角为90°,正确;
②
•
>0是向量
,
的夹角为锐角的充要条件,不正确,当<
,
>=0时也满足条件,因此不正确;
③将函数y=sin(2x-
)的图象按向量
=(-
,0)平移,得到的y=sin[2(x+
)-
]=sin2x,因此其图象对应的函数表达式为y=sin2x,正确.
综上可得:正确的命题是①③.
故选:C.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
②
| a |
| b |
| a |
| b |
| a |
| b |
③将函数y=sin(2x-
| π |
| 3 |
| a |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
综上可得:正确的命题是①③.
故选:C.
点评:本题考查了简易逻辑的判定、数量积运算性质、向量夹角公式、向量的平移变换,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
已知点P为椭圆
+y2=1上的一点,F1,F2是椭圆的焦点,且∠F1PF2=
,则△F1PF2的面积为( )
| x2 |
| 4 |
| π |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
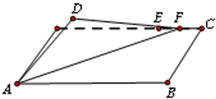 如图,在长方形ABCD中,AB=4,BC=1,E为DC的四等分点(靠近C处),F为线段EC上一动点(包括端点),现将△AFD沿AF折起,使D点在平面内的射影恰好落在边AB上,则当F运动时,二面角D-AF-B的平面角余弦值的变化范围为
如图,在长方形ABCD中,AB=4,BC=1,E为DC的四等分点(靠近C处),F为线段EC上一动点(包括端点),现将△AFD沿AF折起,使D点在平面内的射影恰好落在边AB上,则当F运动时,二面角D-AF-B的平面角余弦值的变化范围为