题目内容
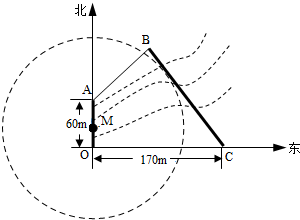 如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=| 4 |
| 3 |
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
考点:圆的切线方程,直线与圆的位置关系
专题:直线与圆
分析:(1)在四边形AOCB中,过B作BE⊥OC于E,过A作AF⊥BE于F,设出AF,然后通过解直角三角形列式求解BE,进一步得到CE,然后由勾股定理得答案;
(2)设BC与⊙M切于Q,延长QM、CO交于P,设OM=xm,把PC、PQ用含有x的代数式表示,再结合古桥两端O和A到该圆上任意一点的距离均不少于80m列式求得x的范围,得到x取最小值时圆的半径最大,即圆形保护区的面积最大.
(2)设BC与⊙M切于Q,延长QM、CO交于P,设OM=xm,把PC、PQ用含有x的代数式表示,再结合古桥两端O和A到该圆上任意一点的距离均不少于80m列式求得x的范围,得到x取最小值时圆的半径最大,即圆形保护区的面积最大.
解答:
解:(1)如图,

过B作BE⊥OC于E,过A作AF⊥BE于F,
∵∠ABC=90°,∠BEC=90°,
∴∠ABF=∠BCE,
∴tan∠ABF=tan∠BCO=
.
设AF=4x(m),则BF=3x(m).
∵∠AOE=∠AFE=∠OEF=90°,
∴OE=AF=4x(m),EF=AO=60(m),
∴BE=(3x+60)m.
∵tan∠BCO=
,
∴CE=
BE=(
x+45)(m).
∴OC=(4x+
x+45)(m).
∴4x+
x+45=170,
解得:x=20.
∴BE=120m,CE=90m,
则BC=150m;
(2)如图,
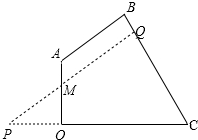
设BC与⊙M切于Q,延长QM、CO交于P,
∵∠POM=∠PQC=90°,
∴∠PMO=∠BCO.
设OM=xm,则OP=
xm,PM=
xm.
∴PC=(
x+170)m,PQ=(
x+136)m.
设⊙M半径为R,
∴R=MQ=(
x+136-
x)m=(136-
x)m.
∵A、O到⊙M上任一点距离不少于80m,
则R-AM≥80,R-OM≥80,
∴136-
x-(60-x)≥80,136-
x-x≥80.
解得:10≤x≤35.
∴当且仅当x=10时R取到最大值.
∴OM=10m时,保护区面积最大.

过B作BE⊥OC于E,过A作AF⊥BE于F,
∵∠ABC=90°,∠BEC=90°,
∴∠ABF=∠BCE,
∴tan∠ABF=tan∠BCO=
| 4 |
| 3 |
设AF=4x(m),则BF=3x(m).
∵∠AOE=∠AFE=∠OEF=90°,
∴OE=AF=4x(m),EF=AO=60(m),
∴BE=(3x+60)m.
∵tan∠BCO=
| 4 |
| 3 |
∴CE=
| 3 |
| 4 |
| 9 |
| 4 |
∴OC=(4x+
| 9 |
| 4 |
∴4x+
| 9 |
| 4 |
解得:x=20.
∴BE=120m,CE=90m,
则BC=150m;
(2)如图,

设BC与⊙M切于Q,延长QM、CO交于P,
∵∠POM=∠PQC=90°,
∴∠PMO=∠BCO.
设OM=xm,则OP=
| 4 |
| 3 |
| 5 |
| 3 |
∴PC=(
| 4 |
| 3 |
| 16 |
| 15 |
设⊙M半径为R,
∴R=MQ=(
| 16 |
| 15 |
| 5 |
| 3 |
| 3 |
| 5 |
∵A、O到⊙M上任一点距离不少于80m,
则R-AM≥80,R-OM≥80,
∴136-
| 3 |
| 5 |
| 3 |
| 5 |
解得:10≤x≤35.
∴当且仅当x=10时R取到最大值.
∴OM=10m时,保护区面积最大.
点评:本题考查圆的切线,考查了直线与圆的位置关系,解答的关键在于对题意的理解,是中档题.

练习册系列答案
相关题目
设
,
,
是非零向量,已知命题p:若
•
=0,
•
=0,则
•
=0;命题q:若
∥
,
∥
,则
∥
,则下列命题中真命题是( )
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| A、p∨q |
| B、p∧q |
| C、(¬p)∧(¬q) |
| D、p∨(¬q) |
设x,y满足约束条件
,则z=x+2y的最大值为( )
|
| A、8 | B、7 | C、2 | D、1 |
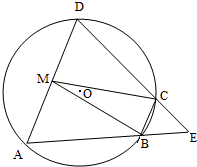 如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.