题目内容
设
,
,
是非零向量,已知命题p:若
•
=0,
•
=0,则
•
=0;命题q:若
∥
,
∥
,则
∥
,则下列命题中真命题是( )
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| A、p∨q |
| B、p∧q |
| C、(¬p)∧(¬q) |
| D、p∨(¬q) |
考点:复合命题的真假,平行向量与共线向量
专题:简易逻辑
分析:根据向量的有关概念和性质分别判断p,q的真假,利用复合命题之间的关系即可得到结论.
解答:
解:若
•
=0,
•
=0,则
•
=
•
,即(
-
)•
=0,则
•
=0不一定成立,故命题p为假命题,
若
∥
,
∥
,则
∥
平行,故命题q为真命题,
则p∨q,为真命题,p∧q,(¬p)∧(¬q),p∨(¬q)都为假命题,
故选:A.
| a |
| b |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| b |
| a |
| c |
若
| a |
| b |
| b |
| c |
| a |
| c |
则p∨q,为真命题,p∧q,(¬p)∧(¬q),p∨(¬q)都为假命题,
故选:A.
点评:本题主要考查复合命题之间的判断,利用向量的有关概念和性质分别判断p,q的真假是解决本题的关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
命题“?x∈[0,+∞),x3+x≥0”的否定是( )
| A、?x∈(-∞,0),x3+x<0 |
| B、?x∈(-∞,0),x3+x≥0 |
| C、?x0∈[0,+∞),x03+x0<0 |
| D、?x0∈[0,+∞),x03+x0≥0 |
设{an}是公比为q的等比数列,则“q>1”是“{an}”为递增数列的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则△OAB的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
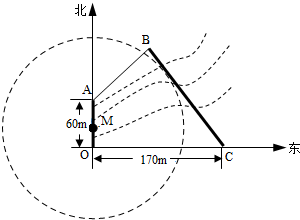 如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=