题目内容
已知函数y=f（x）的周期为2，当x∈[-1，1]时，f（x）=x2，那么函数y=f（x）的图象与函数y=|log4x|的图象的交点共有（ ）
| A、4个 | B、3个 | C、2个 | D、1个 |
考点：函数的周期性,根的存在性及根的个数判断
专题：作图题
分析：由函数的性质和对称性，作出函数的图象可得交点的个数，可得结论．
解答：
解：由y=f（x）的周期为2，当x∈[-1，1]时，f（x）=x2，
可作出函数的图象，由对称可得函数y=|log4x|的图象，
数形结合可得函数图象的交点为4个，
故选：A
可作出函数的图象，由对称可得函数y=|log4x|的图象，
数形结合可得函数图象的交点为4个，
故选：A
点评：本题考查函数图象的交点，涉及函数的周期性和对称性，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
设{an}是公比为q的等比数列，则“q＞1”是“{an}”为递增数列的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设F为抛物线C：y2=3x的焦点，过F且倾斜角为30°的直线交C于A，B两点，O为坐标原点，则△OAB的面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={-2，0，2}，B={x|x2-x-2=0}，则A∩B=（ ）
| A、∅ | B、{2} |
| C、{0} | D、{-2} |
设F为抛物线C：y2=3x的焦点，过F且倾斜角为30°的直线交于C于A，B两点，则|AB|=（ ）
A、
| ||||
| B、6 | ||||
| C、12 | ||||
D、7
|
设点M（x0，1），若在圆O：x2+y2=1上存在点N，使得∠OMN=45°，则x0的取值范围是（ ）
| A、[-1，1] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|
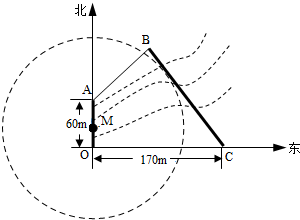如图，为保护河上古桥OA，规划建一座新桥BC，同时设立一个圆形保护区，规划要求：新桥BC与河岸AB垂直；保护区的边界为圆心M在线段OA上并与BC相切的圆，且古桥两端O和A到该圆上任意一点的距离均不少于80m，经测量，点A位于点O正北方向60m处，点C位于点O正东方向170m处（OC为河岸），tan∠BCO=