题目内容
若(ax2+
)6的展开式中x3项的系数为20,则a2+b2的最小值为 .
| b |
| x |
考点:二项式系数的性质,基本不等式
专题:二项式定理
分析:利用二项式定理的展开式的通项公式,通过x幂指数为3,求出ab关系式,然后利用基本不等式求解表达式的最小值.
解答:
解:(ax2+
)6的展开式中x3项的系数为20,
所以Tr+1=
(ax2)6-r(
)r=
a6-rbrx12-3r,
令12-3r=3,∴r=3,
a3b3=20,
∴ab=1,
a2+b2≥2ab=2,当且仅当a=b=1时取等号.
a2+b2的最小值为:2.
故答案为:2.
| b |
| x |
所以Tr+1=
| C | r 6 |
| b |
| x |
| C | r 6 |
令12-3r=3,∴r=3,
| C | 3 6 |
∴ab=1,
a2+b2≥2ab=2,当且仅当a=b=1时取等号.
a2+b2的最小值为:2.
故答案为:2.
点评:本题考查二项式定理的应用,基本不等式的应用,基本知识的考查.

练习册系列答案
相关题目
执行如图所示的程序框图,若输出k的值为6,则判断框内可填入的条件是( )


A、s>
| ||
B、s>
| ||
C、s>
| ||
D、s>
|
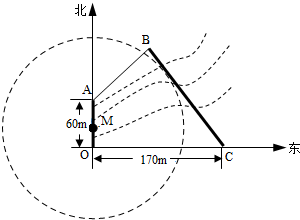 如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=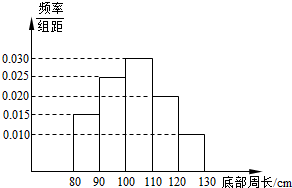 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有
为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有