ЬтФПФкШн
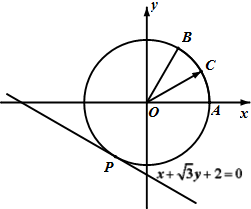 ШчЭМЃЌдВOгыжБЯпx+
ШчЭМЃЌдВOгыжБЯпx+| 3 |
| 3 |
| OC |
| OA |
| OB |
ЃЈ1ЃЉЧѓдВOЕФЗНГЬМАЧњЯпІЃЕФЙьМЃЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯпy=xКЭy=-xЗжБ№НЛЧњЯпІЃгкЕуAЁЂCКЭBЁЂDЃЌЧѓЫФБпаЮABCDЕФжмГЄЃЛ
ЃЈ3ЃЉвбжЊЧњЯпІЃЮЊЭждВЃЌаДГіЭждВІЃЕФЖдГЦжсЁЂЖЅЕузјБъЁЂЗЖЮЇКЭНЙЕузјБъЃЎ
ПМЕуЃКжБЯпгыдВзЖЧњЯпЕФзлКЯЮЪЬт
зЈЬтЃКМЦЫуЬт,дВзЖЧњЯпЕФЖЈвхЁЂаджЪгыЗНГЬ
ЗжЮіЃКЃЈ1ЃЉЧѓГідВOЕФАыОЖЃЌаДГідВOЕФЗНГЬЃЌРћгУ
=x
+y
ЃЌЧѓГіЧњЯпІЃЕФЗНГЬЃЎ
ЃЈ2ЃЉРћгУжБЯпгыЧњЯпЗНГЬСЊСЂЃЌ
ЃЌЧѓГіAЃЌCЃЌBЃЌDЃЌШЛКѓЧѓГіЫФБпаЮABCDЕФжмГЄЃЎ
ЃЈ3ЃЉЩшЧњЯпІЃЩЯШЮвЛЕуЕФзјБъЮЊPЃЈx0ЃЌy0ЃЉЃЌЕуPЙигкжБЯпy=xЕФЖдГЦЕуЮЊP1ЃЈy0ЃЌx0ЃЉЃЌЫЕУїЕуP1дкЧњЯпІЃЩЯЃЌЙЪЧњЯпІЃЙигкжБЯпy=xЖдГЦЃЌЧњЯпІЃЙигкжБЯпy=-xКЭдЕуЖдГЦЃЎЧѓГіx2+y2+xy=1КЭжБЯпy=-xЕФНЛЕузјБъЮЊA1ЃЌA2ЃЌЧѓНтМДПЩЃЎ
| OC |
| OA |
| OB |
ЃЈ2ЃЉРћгУжБЯпгыЧњЯпЗНГЬСЊСЂЃЌ
|
ЃЈ3ЃЉЩшЧњЯпІЃЩЯШЮвЛЕуЕФзјБъЮЊPЃЈx0ЃЌy0ЃЉЃЌЕуPЙигкжБЯпy=xЕФЖдГЦЕуЮЊP1ЃЈy0ЃЌx0ЃЉЃЌЫЕУїЕуP1дкЧњЯпІЃЩЯЃЌЙЪЧњЯпІЃЙигкжБЯпy=xЖдГЦЃЌЧњЯпІЃЙигкжБЯпy=-xКЭдЕуЖдГЦЃЎЧѓГіx2+y2+xy=1КЭжБЯпy=-xЕФНЛЕузјБъЮЊA1ЃЌA2ЃЌЧѓНтМДПЩЃЎ
НтД№ЃК
НтЃКЃЈ1ЃЉгЩЬтвтдВOЕФАыОЖr=
=1ЃЌ
ЙЪдВOЕФЗНГЬЮЊx2+y2=1ЃЎЁЃЈ2ЗжЃЉ
гЩ
=x
+y
ЕУЃЌ
2=(x
+y
)2ЃЌ
МД
2=x2
2+y2
2+2xy|
||
|cos60ЁуЃЌ
ЕУx2+y2+xy=1ЃЈxЃЌyЁЪ[-
ЃЌ
]ЃЉЮЊЧњЯпІЃЕФЗНГЬЃЎЃЈЮДаДxЃЌyЗЖЮЇВЛПлЗжЃЉЁЃЈ4ЗжЃЉ
ЃЈ2ЃЉгЩ
НтЕУЃК
Лђ
ЃЌ
ЫљвдЃЌAЃЈ
ЃЌ
ЃЉЃЌCЃЈ-
ЃЌ-
ЃЉ
ЭЌРэЃЌПЩЧѓЕУBЃЈ1ЃЌ-1ЃЉЃЌDЃЈ-1ЃЌ1ЃЉ
ЫљвдЃЌЫФБпаЮABCDЕФжмГЄЮЊЃК
ЃЈ3ЃЉЧњЯпІЃЕФЗНГЬЮЊx2+y2+xy=1ЃЈxЃЌyЁЪ[-
ЃЌ
]ЃЉЃЌ
ЫќЙигкжБЯпy=xЁЂy=-xКЭдЕуЖдГЦЃЌЯТУцжЄУїЃК
ЩшЧњЯпІЃЩЯШЮвЛЕуЕФзјБъЮЊPЃЈx0ЃЌy0ЃЉЃЌдђx02+y02+x0y0=1ЃЌ
ЕуPЙигкжБЯпy=xЕФЖдГЦЕуЮЊP1ЃЈy0ЃЌx0ЃЉЃЌЯдШЛy02+x02+y0x0=1ЃЌ
ЫљвдЕуP1дкЧњЯпІЃЩЯЃЌЙЪЧњЯпІЃЙигкжБЯпy=xЖдГЦЃЌ
ЭЌРэЧњЯпІЃЙигкжБЯпy=-xКЭдЕуЖдГЦЃЎ
ПЩвдЧѓЕУx2+y2+xy=1КЭжБЯпy=xЕФНЛЕузјБъЮЊB1(-
ЃЌ-
)ЃЌB2(
ЃЌ
)ЃЌ
x2+y2+xy=1КЭжБЯпy=-xЕФНЛЕузјБъЮЊA1ЃЈ-1ЃЌ1ЃЉЃЌA2ЃЈ1ЃЌ-1ЃЉЃЌ
Ёр|OA1|=
ЃЌ|OB1|=
ЃЌЁр
=
ЃЌ
Ёр
=
ЃЎ
дкy=-xЩЯШЁЕуF1(-
ЃЌ
)ЃЌF2(
ЃЌ-
)ЃЎ
ЧњЯпІЃЮЊЭждВЃК
ЦфНЙЕузјБъЮЊF1(-
ЃЌ
)ЃЌF2(
ЃЌ-
)ЃЎ
| 2 | ||||
|
ЙЪдВOЕФЗНГЬЮЊx2+y2=1ЃЎЁЃЈ2ЗжЃЉ
гЩ
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
МД
| OC |
| OA |
| OB |
| OA |
| OB |
ЕУx2+y2+xy=1ЃЈxЃЌyЁЪ[-
2
| ||
| 3 |
2
| ||
| 3 |
ЃЈ2ЃЉгЩ
|
|
|
ЫљвдЃЌAЃЈ
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
ЭЌРэЃЌПЩЧѓЕУBЃЈ1ЃЌ-1ЃЉЃЌDЃЈ-1ЃЌ1ЃЉ
ЫљвдЃЌЫФБпаЮABCDЕФжмГЄЮЊЃК
| 17 |
| 9 |
ЃЈ3ЃЉЧњЯпІЃЕФЗНГЬЮЊx2+y2+xy=1ЃЈxЃЌyЁЪ[-
2
| ||
| 3 |
2
| ||
| 3 |
ЫќЙигкжБЯпy=xЁЂy=-xКЭдЕуЖдГЦЃЌЯТУцжЄУїЃК
ЩшЧњЯпІЃЩЯШЮвЛЕуЕФзјБъЮЊPЃЈx0ЃЌy0ЃЉЃЌдђx02+y02+x0y0=1ЃЌ
ЕуPЙигкжБЯпy=xЕФЖдГЦЕуЮЊP1ЃЈy0ЃЌx0ЃЉЃЌЯдШЛy02+x02+y0x0=1ЃЌ
ЫљвдЕуP1дкЧњЯпІЃЩЯЃЌЙЪЧњЯпІЃЙигкжБЯпy=xЖдГЦЃЌ
ЭЌРэЧњЯпІЃЙигкжБЯпy=-xКЭдЕуЖдГЦЃЎ
ПЩвдЧѓЕУx2+y2+xy=1КЭжБЯпy=xЕФНЛЕузјБъЮЊB1(-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
x2+y2+xy=1КЭжБЯпy=-xЕФНЛЕузјБъЮЊA1ЃЈ-1ЃЌ1ЃЉЃЌA2ЃЈ1ЃЌ-1ЃЉЃЌ
Ёр|OA1|=
| 2 |
| ||
| 3 |
| |OA1|2-|OB1|2 |
2
| ||
| 3 |
Ёр
| ||
|
| ||
| 3 |
дкy=-xЩЯШЁЕуF1(-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
ЧњЯпІЃЮЊЭждВЃК
ЦфНЙЕузјБъЮЊF1(-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
ЕуЦРЃКБОЬтПМВщдВЕФЗНГЬвдМАЧњЯпЙьМЃЗНГЬЕФЧѓЗЈЃЌжБЯпгыЭждВЕФЮЛжУЙиЯЕЕФгІгУЃЌЭждВЕФЛљБОжЊЪЖЕФгІгУЃЌПМВщМЦЫуФмСІЃЎ

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП
вбжЊМЏКЯM={x|xЃМ1}ЃЌМЏКЯN={y|yЃО0}ЃЌдђMЁЩN=ЃЈЁЁЁЁЃЉ
| AЁЂ{x|xЃМ1} |
| BЁЂ{x|xЃО1} |
| CЁЂ{x|0ЃМxЃМ1} |
| DЁЂ∅ |
ШчЙћжБЯп3x-
y+m=0гыЫЋЧњЯпCЃК
-
=1ЃЈaЃО0ЃЌbЃО0ЃЉКугаСНИіЙЋЙВЕуЃЌдђЫЋЧњЯпCЕФРыаФТЪЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| AЁЂЃЈ1ЃЌ2ЃЉ |
| BЁЂЃЈ2ЃЌ+ЁоЃЉ |
| CЁЂЃЈ1ЃЌ2] |
| DЁЂ[2ЃЌ+ЁоЃЉ |
ШчЭМЫљЪОЕФГЬађПђЭМЃЌФмЪЙЪфШыЕФxжЕгыЪфГіЕФyжЕЯрЕШЕФxжЕИіЪ§ЮЊЃЈЁЁЁЁЃЉ
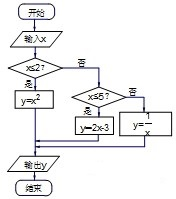

| AЁЂ1 | BЁЂ2 | CЁЂ3 | DЁЂ4 |
 ШчЭМЃЌвбжЊжБЯпl1ЃКy=4x+mЃЌЃЈmЃМ0ЃЉгыХзЮяЯп
ШчЭМЃЌвбжЊжБЯпl1ЃКy=4x+mЃЌЃЈmЃМ0ЃЉгыХзЮяЯп