题目内容
已知过点P（2，-1）的直线l交椭圆
+
=1于M、N两点，B（0，2）是椭圆的一个顶点，若线段MN的中点恰为点P．
（Ⅰ）求直线l的方程；
（Ⅱ）求△BMN的面积．
| x 2 |
| 8 |
| y 2 |
| 4 |
（Ⅰ）求直线l的方程；
（Ⅱ）求△BMN的面积．
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：（Ⅰ）设M（x1，y1），N（x2，y2），利用点差法，求出直线的斜率，即可求直线l的方程；
（Ⅱ）y=x-3代入椭圆方程，利用韦达定理求出|MN|，求出B（0，2）到直线y=x-3的距离，即可求△BMN的面积．
（Ⅱ）y=x-3代入椭圆方程，利用韦达定理求出|MN|，求出B（0，2）到直线y=x-3的距离，即可求△BMN的面积．
解答：
解：（Ⅰ）设M（x1，y1），N（x2，y2），则
+
=1，
+
=1，
∵线段MN的中点恰为点P，
∴两式相减可得
+
=1，
∴k=
=1
∴可得直线l的方程为y=x-3；
（Ⅱ）y=x-3代入椭圆方程，可得3x2-12x+10=0，
∴x1+x2=4，x1x2=
，
∴|MN|=
|x1-x2|=
，
∵B（0，2）到直线y=x-3的距离为d=
=
，
∴△BMN的面积
|MN|d=
．
| x12 |
| 8 |
| y12 |
| 4 |
| x22 |
| 8 |
| y22 |
| 4 |
∵线段MN的中点恰为点P，
∴两式相减可得
| 4(x2-x1) |
| 8 |
| -2(y2-y1) |
| 4 |
∴k=
| y2-y1 |
| x2-x1 |
∴可得直线l的方程为y=x-3；
（Ⅱ）y=x-3代入椭圆方程，可得3x2-12x+10=0，
∴x1+x2=4，x1x2=
| 10 |
| 3 |
∴|MN|=
| 1+k2 |
4
| ||
| 3 |
∵B（0，2）到直线y=x-3的距离为d=
| 5 | ||
|
5
| ||
| 2 |
∴△BMN的面积
| 1 |
| 2 |
5
| ||
| 3 |
点评：本题考查点差法的运用，考查三角形面积的计算，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
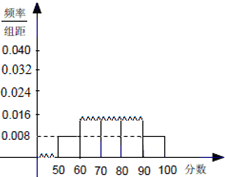随机抽取某中学高一级学生的一次数学统测成绩得到一样本，其分组区间和频数是：[50，60），2；[60，70），7；[70，80），10；[80，90），x；[90，100]，2．其频率分布直方图受到破坏，可见部分如图所示，据此解答如下问题．
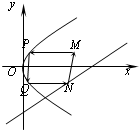如图，从点M（x0，4）发出的光线，沿平行于抛物线y2=8x的对称轴方向射向此抛物线上的点P，经抛物线反射后，穿过焦点射向抛物线上的点Q，再经抛物线反射后射向直线l：x-y-10=0上的点N，经直线反射后又回到点M，则x0等于（ ）
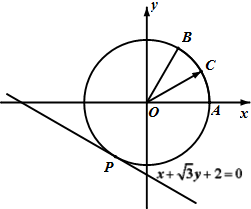如图，圆O与直线x+