题目内容
求y=
的值域.
| x |
| 1+x2 |
考点:函数的值域
专题:函数的性质及应用
分析:函数y=
可化为yx2-x+y=0,讨论x=0时,y=0,y≠0时,关于x的一元二次方程yx2-x+y=0有实数根;应用判别式△≥0,可求出y的值域.
| x |
| 1+x2 |
解答:
解:∵函数y=
(其中x∈R),
∴y(1+x2)=x,
即yx2-x+y=0;
当x=0时,y=0;
y≠0时,关于x的一元二次方程yx2-x+y=0有实数根;
∴判别式(-1)2-4y•y≥0,
解得:-
≤y≤
且y≠0;
综上,函数y的值域是[-
,
].
| x |
| 1+x2 |
∴y(1+x2)=x,
即yx2-x+y=0;
当x=0时,y=0;
y≠0时,关于x的一元二次方程yx2-x+y=0有实数根;
∴判别式(-1)2-4y•y≥0,
解得:-
| 1 |
| 2 |
| 1 |
| 2 |
综上,函数y的值域是[-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了求函数的值域问题,解题时根据函数解析式的特点,应用判别式法,容易求出值域.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
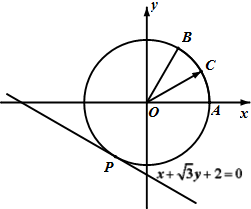 如图,圆O与直线x+
如图,圆O与直线x+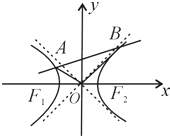 如图,F1,F2是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b与圆O相切,并与双曲线交于A、B两点.
如图,F1,F2是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b与圆O相切,并与双曲线交于A、B两点.