题目内容
已知双曲线C:
-
=1(a,b>0)的一条渐近线方程是y=
x,它的一个焦点在抛物线y2=4
x的准线上,点A(x1,y1),B(x2,y2)是双曲线C右支上相异两点,且满足x1+x2=6,D为线段AB的中点,直线AB的斜率为k.
(Ⅰ)求双曲线C的方程;
(Ⅱ)用k表示点D的坐标;
(Ⅲ)若k>0,AB的中垂线交x轴于点M,直线AB交x轴于点N,求△DMN的面积的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 5 |
(Ⅰ)求双曲线C的方程;
(Ⅱ)用k表示点D的坐标;
(Ⅲ)若k>0,AB的中垂线交x轴于点M,直线AB交x轴于点N,求△DMN的面积的取值范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由题设条件推导出
=
,
=
,由此能求出双曲线C的方程.
(Ⅱ)法一:设直线AB的方程为y=kx+d,k≠±
,k≠0,代入方程
-y2=1(x≥2),得(4k2-1)x2+8kdx+4(d2+1)=0,用根的判别式和韦达定理求出D(3,
),由此能求出k的取值范围.
法二:利用点差法求出D(3,
),由此能求出k的取值范围.
(Ⅲ)方程y=kx+
中,令y=0,得xN=3-
,由已知条件求出M(
,0),由此能求出△DMN的面积的取值范围.
| b |
| a |
| 1 |
| 2 |
| a2+b2 |
| 5 |
(Ⅱ)法一:设直线AB的方程为y=kx+d,k≠±
| 1 |
| 2 |
| x2 |
| 4 |
| 3 |
| 4k |
法二:利用点差法求出D(3,
| 3 |
| 4k |
(Ⅲ)方程y=kx+
| 3(1-4k2) |
| 4k |
| 3 |
| 4k2 |
| 15 |
| 4 |
解答:
解:(Ⅰ)∵双曲线C:
-
=1(a,b>0)的一条渐近线方程是y=
x,
它的一个焦点在抛物线y2=4
x的准线上,
∴
=
,
=
,
解得a=2,b=1,
∴双曲线C的方程为
-y2=1.…(3分)
(Ⅱ)解法一:设直线AB的方程为y=kx+d,k≠±
,k≠0,
代入方程
-y2=1(x≥2),
得(4k2-1)x2+8kdx+4(d2+1)=0,
当△>0时记两个实数根为x1,x2,
则x1+x2=
=6,x1x2=
>0,
∴d=
,
∴AB的方程为y=kx+
,
把x=3代入得yD=
,∴D(3,
),…(6分)
下求k的取值范围:法一:由△>0,得d2+1-4k2>0,
即
+1-4k2>0,
而1-4k2<0,所以
+1<0,化简得|k|>
;…(7分)
法二:在
-y2=1中令x=3,得y2=
,∴|yD|<
,
即|
|<
,所以|k|>
,
再结合|k|>
,得|k|>
.…(7分)
(Ⅱ)解法二:
=4
+4,
=4
+4,
两式相减得6(x1-x2)=8yD•(y1-y2),
∵k=
,∴yD=
,∴D(3,
),…(6分)
下求k的取值范围:法一:由△>0,得d2+1-4k2>0,
即
+1-4k2>0,
而1-4k2<0,所以
+1<0,化简得|k|>
;…(7分)
法二:在
-y2=1中令x=3,得y2=
,∴|yD|<
,
即|
|<
,所以|k|>
,
再结合|k|>
,得|k|>
.…(7分)
(Ⅲ)由(Ⅱ)知方程y=kx+
中,
令y=0,得xN=3-
,
设点M的坐标为(m,0),由kMD=-
,得m=
,
∴M(
,0),∴|MN|=|xM-xN|=
(1+
),
∴S△DMN=
•
(1+
)•
=
(1+
)
,…(9分)
∵k>0,∴k>
,
∴0<
<
,∴S△DMN∈(0,
).…(11分)
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
它的一个焦点在抛物线y2=4
| 5 |
∴
| b |
| a |
| 1 |
| 2 |
| a2+b2 |
| 5 |
解得a=2,b=1,
∴双曲线C的方程为
| x2 |
| 4 |
(Ⅱ)解法一:设直线AB的方程为y=kx+d,k≠±
| 1 |
| 2 |
代入方程
| x2 |
| 4 |
得(4k2-1)x2+8kdx+4(d2+1)=0,
当△>0时记两个实数根为x1,x2,
则x1+x2=
| 8kd |
| 1-4k2 |
| 4(d2+1) |
| 4k2-1 |
∴d=
| 3(1-4k2) |
| 4k |
∴AB的方程为y=kx+
| 3(1-4k2) |
| 4k |
把x=3代入得yD=
| 3 |
| 4k |
| 3 |
| 4k |
下求k的取值范围:法一:由△>0,得d2+1-4k2>0,
即
| 9(1-4k2)2 |
| 16k2 |
而1-4k2<0,所以
| 9(1-4k2) |
| 16k2 |
3
| ||
| 10 |
法二:在
| x2 |
| 4 |
| 5 |
| 4 |
| ||
| 2 |
即|
| 3 |
| 4k |
| ||
| 2 |
3
| ||
| 10 |
再结合|k|>
| 1 |
| 2 |
3
| ||
| 10 |
(Ⅱ)解法二:
| x | 2 1 |
| y | 2 1 |
| x | 2 2 |
| y | 2 2 |
两式相减得6(x1-x2)=8yD•(y1-y2),
∵k=
| y1-y2 |
| x1-x2 |
| 3 |
| 4k |
| 3 |
| 4k |
下求k的取值范围:法一:由△>0,得d2+1-4k2>0,
即
| 9(1-4k2)2 |
| 16k2 |
而1-4k2<0,所以
| 9(1-4k2) |
| 16k2 |
3
| ||
| 10 |
法二:在
| x2 |
| 4 |
| 5 |
| 4 |
| ||
| 2 |
即|
| 3 |
| 4k |
| ||
| 2 |
3
| ||
| 10 |
再结合|k|>
| 1 |
| 2 |
3
| ||
| 10 |
(Ⅲ)由(Ⅱ)知方程y=kx+
| 3(1-4k2) |
| 4k |
令y=0,得xN=3-
| 3 |
| 4k2 |
设点M的坐标为(m,0),由kMD=-
| 1 |
| k |
| 15 |
| 4 |
∴M(
| 15 |
| 4 |
| 3 |
| 4 |
| 1 |
| k2 |
∴S△DMN=
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| k2 |
| 3 |
| 4k |
| 9 |
| 32 |
| 1 |
| k2 |
| 1 |
| k |
∵k>0,∴k>
3
| ||
| 10 |
∴0<
| 1 |
| k |
2
| ||
| 3 |
29
| ||
| 48 |
点评:本题考查双曲线方程的求法,考查点的坐标的求法,考查三角形面积的取值范围的求法,解题时要熟练掌握圆锥曲线的简单性质,注意等价转化思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
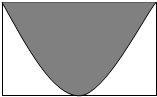 如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60颗豆子落在阴影部分内,则用随机摸拟的方法可以估计图中阴影部分的面积为( )
如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60颗豆子落在阴影部分内,则用随机摸拟的方法可以估计图中阴影部分的面积为( ) 如图所示,一游泳者自游泳池边AB上的D点,沿DC方向游了10米,∠CDB=60°,然后任意选择一个方向并沿此方向继续游,则他再游不超过10米就能够回到游泳池AB边的概率是( )
如图所示,一游泳者自游泳池边AB上的D点,沿DC方向游了10米,∠CDB=60°,然后任意选择一个方向并沿此方向继续游,则他再游不超过10米就能够回到游泳池AB边的概率是( )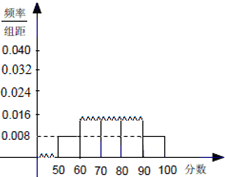 随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是:[50,60),2;[60,70),7;[70,80),10;[80,90),x;[90,100],2.其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题.
随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是:[50,60),2;[60,70),7;[70,80),10;[80,90),x;[90,100],2.其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题.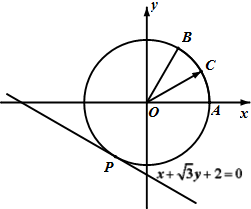 如图,圆O与直线x+
如图,圆O与直线x+