题目内容
抛物线C:y2=2px(p>0)的焦点为F,抛物线C上点M的横坐标为2,且|MF|=3.
(1)求抛物线C的方程;
(2)过焦点F作两条相互垂直的直线,分别与抛物线C交于M、N和P、Q四点,求四边形MPNQ面积的最小值.
(1)求抛物线C的方程;
(2)过焦点F作两条相互垂直的直线,分别与抛物线C交于M、N和P、Q四点,求四边形MPNQ面积的最小值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)利用抛物线的定义直接求抛物线C的方程;
(2)过焦点F作两条相互垂直的直线,设MN:x=my+1,PQ:x=-
y+1(m≠0),联立直线与抛物线方程组成方程组,利用弦长公式,求出MN,PQ,推出四边形MPNQ的面积的表达式,利用基本不等式求四边形MPNQ面积的最小值.
(2)过焦点F作两条相互垂直的直线,设MN:x=my+1,PQ:x=-
| 1 |
| m |
解答:
解:(1)由已知:2+
=3 ∴P=3
故抛物线C的方程为:y2=4x…(4分)
(2)由(1)知:F(1,0)
设MN:x=my+1,PQ:x=-
y+1(m≠0)…(6分)
由
得:y2-4my-4=0
∵△=16m2+16=16(m2+1)>0
∴|MN|=
•4•
=4(m2+1)…(8分)
同理:|PQ|=4(
+1)…(10分).
∴四边形MPNQ的面积:S=
|MN||PQ|=8(m2+1)(
+1)=8(m2+
+2)≥32
(当且仅当m2=
即:m=±1时等号成立)
∴四边形MPNQ的面积的最小值为32.…(12分)
| P |
| 2 |
故抛物线C的方程为:y2=4x…(4分)
(2)由(1)知:F(1,0)
设MN:x=my+1,PQ:x=-
| 1 |
| m |
由
|
∵△=16m2+16=16(m2+1)>0
∴|MN|=
| 1+m2 |
| m2+1 |
同理:|PQ|=4(
| 1 |
| m2 |
∴四边形MPNQ的面积:S=
| 1 |
| 2 |
| 1 |
| m2 |
| 1 |
| m2 |
(当且仅当m2=
| 1 |
| m2 |
∴四边形MPNQ的面积的最小值为32.…(12分)
点评:本题考查抛物线的标准方程的求法,直线与抛物线的位置关系的应用,四边形面积的最值以及基本不等式的应用,考查转化思想以及计算能力.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
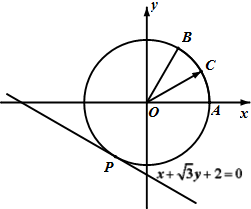 如图,圆O与直线x+
如图,圆O与直线x+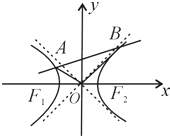 如图,F1,F2是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b与圆O相切,并与双曲线交于A、B两点.
如图,F1,F2是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b与圆O相切,并与双曲线交于A、B两点.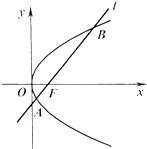 如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A,B两点
如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A,B两点