题目内容
8.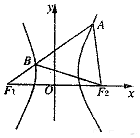 如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 根据双曲线的定义算出△AF1F2中,|AF1|=2a,|AF2|=4a,由△ABF2是等边三角形得∠F1AF2=120°,利用余弦定理算出c2=7a2,结合A(1,$\sqrt{3}$)在双曲线上,即可得出结论.
解答 解:根据双曲线的定义,可得|AF1|-|AF2|=2a,
∵△ABF2是等边三角形,即|AF2|=|AB|
∴|BF1|=2a
又∵|BF2|-|BF1|=2a,
∴|BF2|=|BF1|+2a=4a,
∵△BF1F2中,|BF1|=2a,|BF2|=4a,∠F1BF2=120°
∴|F1F2|2=|BF1|2+|BF2|2-2|BF1|•|BF2|cos120°
即4c2=4a2+16a2-2×2a×4a×(-$\frac{1}{2}$)=28a2,
解得c2=7a2,
∴b2=c2-a2=6a2,所以双曲线方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{6{a}^{2}}$=1,
又A(1,$\sqrt{3}$),在双曲线上,所以$\frac{1}{{a}^{2}}-\frac{3}{6{a}^{2}}$=1,解得a=$\frac{\sqrt{2}}{2}$.
所以△BF1F2的面积为$\frac{1}{2}×2a×4a×sin120°$=$2\sqrt{3}{a}^{2}$=$\sqrt{3}$,
故选C.
点评 本题主要考查双曲线的定义和简单几何性质等知识,根据条件求出a,b的关系是解决本题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
18.函数f(x)=x2-5x+6,x∈[-5,5],在定义域内任取一点x0,使f(x0)≤0的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{4}{5}$ |
3.将向量$\overrightarrow{a_1}=({{x_1},{y_1}}),\overrightarrow{a_2}=({{x_2},{y_2}}),…\overrightarrow{a_n}=({{x_n},{y_n}})$组成的系列称为向量列$\left\{{\overrightarrow{a_n}}\right\}$,并定义向量列$\left\{{\overrightarrow{a_n}}\right\}$的前n项和$\overrightarrow{S_n}=\overrightarrow{a_1}+\overrightarrow{a_2}+…+\overrightarrow{a_n}$.如果一个向量列从第二项起,每一项与前一项的差都是同一个向量,那么称这样的向量列为等差向量列,若向量列$\left\{{\overrightarrow{a_n}}\right\}$是等差向量列,那么下述向量中,与一定平行$\overrightarrow{{S}_{21}}$的向量是( )
| A. | $\overrightarrow{{a_{10}}}$ | B. | $\overrightarrow{{a_{11}}}$ | C. | $\overrightarrow{{a_{20}}}$ | D. | $\overrightarrow{{a_{21}}}$ |
13.函数f(x)=x+cosx在[0,π]上的最小值为( )
| A. | -2 | B. | 0 | C. | -$\frac{1}{2}$ | D. | 1 |
18.已知幂函数f(x)=xα(α为常数)的图象过点$P({2,\frac{1}{2}})$,则f(x)的单调递减区间是( )
| A. | (-∞,0) | B. | (-∞,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-∞,0)与(0,+∞) |
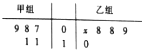 如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.
如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.