题目内容
16.已知向量$\overrightarrow{a}$=(m,-1),$\overrightarrow{b}$=($\frac{1}{2},\frac{\sqrt{3}}{2}$)(1)若m=-$\sqrt{3}$,求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ;
(2)设$\overrightarrow{a}⊥\overrightarrow{b}$.
①求实数m的值;
②若存在非零实数k,t,使得[$\overrightarrow{a}$+(t2-3)$\overrightarrow{b}$]⊥(-k$\overrightarrow{a}$+t$\overrightarrow{b}$),求$\frac{k+{t}^{2}}{t}$的最小值.
分析 (1)由条件利用两个向量的数量积的定义求得cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$的值,可得θ的值.
(2)①利用两个向量垂直的性质,求得m的值.
②根据[$\overrightarrow{a}$+(t2-3)$\overrightarrow{b}$]•(-k$\overrightarrow{a}$+t$\overrightarrow{b}$)=0,求得4k=t(t2-3),从而求得 $\frac{k+{t}^{2}}{t}$=$\frac{{(t+2)}^{2}-7}{4}$,再利用二次函数的性质求得它的最小值.
解答 解:(1)向量$\overrightarrow{a}$=(m,-1),$\overrightarrow{b}$=($\frac{1}{2},\frac{\sqrt{3}}{2}$),若m=-$\sqrt{3}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ,
则有cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{-\sqrt{3}•\frac{1}{2}-1•\frac{\sqrt{3}}{2}}{2•1}$=-$\frac{\sqrt{3}}{2}$,∴θ=$\frac{5π}{6}$.
(2)①设$\overrightarrow{a}⊥\overrightarrow{b}$,则$\overrightarrow{a}•\overrightarrow{b}$=$\frac{m}{2}$-$\frac{\sqrt{3}}{2}$=0,∴m=$\sqrt{3}$.
②由①可得,$\overrightarrow{a}$=($\sqrt{3}$,-1),$\overrightarrow{a}•\overrightarrow{b}$=$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{2}$=0,
若存在非零实数k,t,使得[$\overrightarrow{a}$+(t2-3)$\overrightarrow{b}$]⊥(-k$\overrightarrow{a}$+t$\overrightarrow{b}$),故有[$\overrightarrow{a}$+(t2-3)$\overrightarrow{b}$]•(-k$\overrightarrow{a}$+t$\overrightarrow{b}$)=0,
∴-k${\overrightarrow{a}}^{2}$+[-k(t2-3)+t]$\overrightarrow{a}•\overrightarrow{b}$+t(t2-3)${\overrightarrow{b}}^{2}$=-k•4+0+t(t2-3)=0,∴4k=t(t2-3),
∴$\frac{k+{t}^{2}}{t}$=$\frac{{t}^{2}-3}{4}$+t=$\frac{{t}^{2}+4t-3}{4}$=$\frac{{(t+2)}^{2}-7}{4}$≥-$\frac{7}{4}$,当且仅当t=-2时,取等号,
故$\frac{k+{t}^{2}}{t}$的最小值为-$\frac{7}{4}$.
点评 本题主要考查两个向量的数量积的运算,两个向量垂直的性质,二次函数的性质应用,属于中档题.

| A. | 121 | B. | -74 | C. | 74 | D. | -121 |
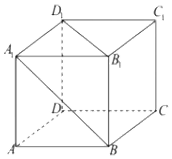
| A. | A1B∥D1B | B. | AC1⊥B1C | ||
| C. | A1B与平面DBD1B1成角为45° | D. | A1B,B1C成角为30° |
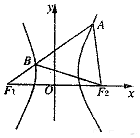 如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
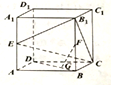 如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.
如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.