题目内容
20.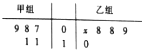 如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.
如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.(1)若乙组同学投篮命中次数的平均数比甲组同学的平均数少1,求x及乙组同学投篮命中次数的方差;
(2)在(1)的条件下,分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名,求这两名同学的投篮命中次数之和为16的概率.
分析 (1)依题意得求出x=6,$\overline{{x}_{乙}}$=$\frac{41}{5}$,由此能求出乙组同学投篮命中次数的方差.
(2)记甲组投篮命中次数低于10次的同学为A1,A2,A3,他们的命中次数分别为9,8,7.乙组投篮命中次数低于10次的同学为B1,B2,B3,B4,他们的命中次数分别为6,8,8,9.由此利用列举法能求出这两名同学的投篮命中次数之和为16的概率.
解答 解:(1)依题意得:$\frac{x+8×2+9+10}{5}$=$\frac{7+8+9+11×2}{5}-1$,
解得x=6,$\overline{{x}_{乙}}$=$\frac{41}{5}$,
∴乙组同学投篮命中次数的方差S2=$\frac{1}{5}$[(6-$\frac{41}{5}$)2+(8-$\frac{41}{5}$)2×2+(9-$\frac{41}{5}$)2+(10-$\frac{41}{5}$)2]=1.76.
(2)记甲组投篮命中次数低于10次的同学为A1,A2,A3,他们的命中次数分别为9,8,7.
乙组投篮命中次数低于10次的同学为B1,B2,B3,B4,他们的命中次数分别为6,8,8,9.
依题意,不同的选取方法有:
(A1,B1),(A1,B2),(A1,B3),(A1,B4),(A2,B1),(A2,B2),(A2,B3),
(A2,B4),(A3,B1),(A3,B2),(A3,B3),(A3,B4)共12种.
设“这两名同学的投篮命中次数之和为16”为事件,
则中恰含有(A2B2),(A2,B3),(A3,B4)共3种.
这两名同学的投篮命中次数之和为16的概率P(C)=$\frac{3}{12}=\frac{1}{4}$.
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

| A. | 121 | B. | -74 | C. | 74 | D. | -121 |
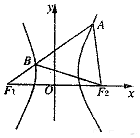 如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
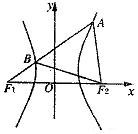 如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,若△ABF2为等边三角形,则双曲线的渐近线的斜率为( )
如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,若△ABF2为等边三角形,则双曲线的渐近线的斜率为( )| A. | ±$\sqrt{3}$ | B. | ±2 | C. | $±\sqrt{6}$ | D. | ±$\sqrt{2}$ |
| A. | 6 | B. | $\sqrt{6}$ | C. | 3 | D. | $\sqrt{3}$ |
| A. | (-∞,e) | B. | (0,e) | C. | (e,+∞) | D. | (-∞,1) |