题目内容
19.从抛物线y2=32x上各点向x轴作垂线,其垂线段中点的轨迹为E.(Ⅰ)求轨迹E的方程;
(Ⅱ)已知直线l:y=k(x-2)(k>0)与轨迹E交于A,B两点,且点F(2,0),若|AF|=2|BF|,求弦AB的长.
分析 (Ⅰ)先设出垂线段的中点为M(x,y),P(x0,y0)是抛物线上的点,把它们坐标之间的关系找出来,代入抛物线的方程即可;
(Ⅱ)根据抛物线的方程求出准线方程,利用抛物线的定义即条件,求出A,B的中点横坐标,即可求出弦AB的长.
解答 解:(Ⅰ)设垂线段的中点M(x,y),P(x0,y0)是抛物线上的点,D(x0,0),
因为M是PD的中点,所以x0=x,y=$\frac{1}{2}$y0,
有x0=x,y0=2y,
因为点P在抛物线上,所以y02=32x,即4y2=32x,
所以y2=8x,所求点M轨迹方程为:y2=8x.
(Ⅱ)抛物线y2=8x的焦点坐标为(2,0),准线方程为x=-2,
设A(x1,y1),B(x2,y2),则
∵|AF|=2|BF|,∴x1+1=2(x2+1),∴x1=2x2+1
∵|y1|=2|y2|,∴x1=4x2,∴x1=2,x2=$\frac{1}{2}$,
∴|AB|=x1+x2+p=$\frac{5}{2}$+4=$\frac{13}{2}$.
点评 本题主要考查求轨迹方程的方法,考查学生分析解决问题的能力,利用抛物线的定义将到焦点的距离转化为到准线的距离是关键,属于中档题.

练习册系列答案
相关题目
19.函数y=x2在P(1,1)处的切线与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线平行,则双曲线的离心率是( )
| A. | 5 | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{3}$ |
11.在(1-x)5+(1-x)6+(1-x)7+(1-x)8的展开式中,含x3的项的系数是( )
| A. | 121 | B. | -74 | C. | 74 | D. | -121 |
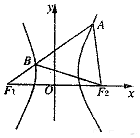 如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )