题目内容
17.在数列{an}中,a1=2,2an+1-2an=1,则S12=57.分析 利用等差数列的通项公式及其前n项和公式即可得出.
解答 解:∵a1=2,2an+1-2an=1,
∴an+1-an=$\frac{1}{2}$,
∴数列{an}是等差数列,首项为2,公差为$\frac{1}{2}$.
其前n项和S12=12×2+$\frac{12×11}{2}$×$\frac{1}{2}$=57.
故答案是:57.
点评 本题考查了等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.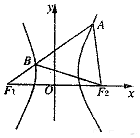 如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )
 如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
5.过抛物线y2=4ax(a>0)的焦点F作斜率为-1的直线l,l与离心率为e的双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({b>0})$的两条渐近线的交点分别为B,C.若xB,xC,xF分别表示B,C,F的横坐标,且$x_F^2=-{x_B}•{x_C}$,则e=( )
| A. | 6 | B. | $\sqrt{6}$ | C. | 3 | D. | $\sqrt{3}$ |
2.已知全集U={1,2,3,4,5,6,7},集合A={1,3,5,6,7},B={1,2,3,4,6,7},则A∩∁UB=( )
| A. | {3,6} | B. | {5} | C. | {2,4} | D. | {2,5} |
7.函数y=x2+ln|x|的图象大致为( )
| A. | 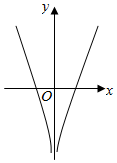 | B. | 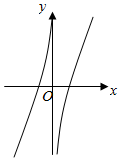 | C. | 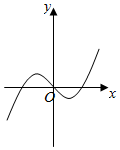 | D. |  |
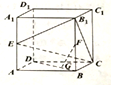 如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.
如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.