题目内容
14.一个由底面是正三角形的三棱柱和三棱锥组成的组合体,其三视图如图所示,则该组合体的体积为( )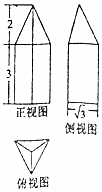
| A. | $\frac{11\sqrt{3}}{3}$ | B. | $\frac{15\sqrt{3}}{4}$ | C. | $\frac{11\sqrt{3}}{4}$ | D. | 5$\sqrt{3}$ |
分析 由三视图可得该组合体是上面为正三棱锥,下面为正三棱柱,其底面的边长为2,高分别为2和3,运用棱锥和棱柱的体积公式计算即可得到所求.
解答  解:该组合体为由底面是正三角形的三棱柱和三棱锥组成的,
解:该组合体为由底面是正三角形的三棱柱和三棱锥组成的,
由侧视图可得底面正三角形的高为$\sqrt{3}$,
可得底面边长为2,
由正视图可得三棱柱的高为3,三棱锥的高为2,
则该组合体的体积为$\frac{1}{3}$×$\frac{1}{2}$×2×$\sqrt{3}$×2+$\frac{1}{2}$×2×$\sqrt{3}$×3=$\frac{11\sqrt{3}}{3}$.
故选:A.
点评 本题考查组合体的体积的求法,注意运用棱柱和棱锥的体积公式,由三视图正确还原几何体的直观图是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.设点P(x,y)在不等式组$\left\{\begin{array}{l}x≥1\\ 2x-y≤0\\ x+y-6≤0\end{array}\right.$所表示的平面区域内,则$z=\frac{9xy}{{9{x^2}+{y^2}}}$的取值范围为( )
| A. | $[{\frac{18}{13},\frac{3}{2}}]$ | B. | $[{\frac{45}{34},\frac{3}{2}}]$ | C. | $[{\frac{45}{34},\frac{18}{13}}]$ | D. | $[{\frac{18}{13},\frac{45}{34}}]$ |
19.已知i是虚数单位,则满足z-i=|1+2i|的复数z在复平面上对应点所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.设函数f(x)的定义域为D,若满足条件:存在[a,b]⊆D,使f(x)在[a,b]上的值域为[$\frac{a}{2}$,$\frac{b}{2}$],则称f(x)为“倍缩函数”.若函数f(x)=lnx+t为“倍缩函数”,则实数t的取值范围是( )
| A. | (-∞,ln2-1) | B. | (-∞,ln2-1] | C. | (1-ln2,+∞) | D. | [1-ln2,+∞) |
3.复数$\frac{1-i}{3+4i}$(其中i是虚数单位)在复平面内对应的点所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |