题目内容
在△ABC中，三个内角A、B、C所对的边分别为a、b、c．若内角A、B、C依次成等差数列，且a和c是-x2+6x-8=0的两根，则S△ABC=（ ）
A、4
| ||
B、3
| ||
C、2
| ||
D、
|
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用等差数列的性质，可得B=60°，由a和c是-x2+6x-8=0的两根，求出a，c，再利用三角形面积公式，可得结论
解答：
解：∵内角A、B、C依次成等差数列，∴B=60°，
∵a和c是-x2+6x-8=0的两根，∴a=2，c=4，
∴S△ABC=
acsinB=
×2×4×
=2
，
故选：C．
∵a和c是-x2+6x-8=0的两根，∴a=2，c=4，
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
故选：C．
点评：本题考查等差数列的性质，考查三角形面积公式，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
函数f（x）=|x+2|的单调递减区间是（ ）
| A、（-∞，-2] |
| B、（-∞，2] |
| C、（-∞，0] |
| D、无减区间 |
已知a，b是正实数，A是a，b的等差中项，G是a，b等比中项，则（ ）
| A、ab≤AG |
| B、ab≥AG |
| C、ab≤|AG| |
| D、ab＞AG |
记a=log2
，b=70.3．c=（
）9.1，则a、b、c的大小关系是（ ）
| 5 |
| 6 |
| 1 |
| 7 |
| A、a＜b＜c |
| B、c＜b＜a |
| C、a＜c＜b |
| D、b＜a＜c |
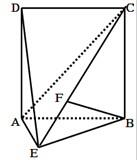如图，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE，求DE与平面AEC所成夹角的正弦值．