题目内容
已知方程a2x+1=x2+x有一实数解x0,且x∈(
,
),求a的范围.
| 1 |
| 4 |
| 1 |
| 2 |
考点:函数的零点
专题:函数的性质及应用
分析:分离参数得出a=
,x∈(
,
),构造函数f(x)=
,x∈(
,
)是单调递增函数,
求出最值,运用2个函数图象的交点问题求解即可.
| 2x+1 | x2+x |
| 1 |
| 4 |
| 1 |
| 2 |
| 2x+1 | x2+x |
| 1 |
| 4 |
| 1 |
| 2 |
求出最值,运用2个函数图象的交点问题求解即可.
解答:
解:∵a2x+1=x2+x,
∴a=
,x∈(
,
),
令f(x)=
,x∈(
,
)根据函数解析式判断f(x)是单调递增函数,
f(
)=(
)
,
f(
)=
,
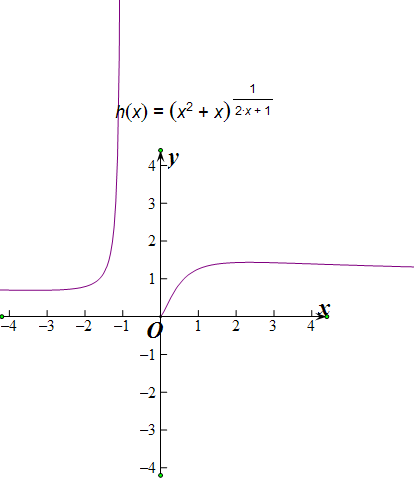
∴y=a与f(x)=
=(x2+x)
,x∈(
,
)有1个交点,
∴(
)
<a<
,
∴a=
| 2x+1 | x2+x |
| 1 |
| 4 |
| 1 |
| 2 |
令f(x)=
| 2x+1 | x2+x |
| 1 |
| 4 |
| 1 |
| 2 |
f(
| 1 |
| 4 |
| 5 |
| 16 |
| 2 |
| 3 |
f(
| 1 |
| 2 |
| ||
| 2 |
∴y=a与f(x)=
| 2x+1 | x2+x |
| 1 |
| 2x+1 |
| 1 |
| 4 |
| 1 |
| 2 |
∴(
| 5 |
| 16 |
| 2 |
| 3 |
| ||
| 2 |

点评:本题考查了复杂函数的单调性,运用分离参数,构造函数,运用单调性判断范围,即可得出所求字母的范围,属于中档题.

练习册系列答案
相关题目
已知集合A={0,1,2},集合B={0,2,4},则A∪B=( )
| A、{0} |
| B、{2} |
| C、{0,2,4} |
| D、{0,1,2,4} |
 如图,边长为2的正方形ACDE所在平面与平面ABC垂直,AD与CE的交点为M,AC⊥BC,且AC=BC,
如图,边长为2的正方形ACDE所在平面与平面ABC垂直,AD与CE的交点为M,AC⊥BC,且AC=BC,