题目内容
设椭圆
+
=1(a>b>0)的左、右焦点分别为F1、F2,右顶点为A,上顶点为B,已知原点O到直线AB的距离为
b
(Ⅰ)求椭圆的离心率;
(Ⅱ)设P为椭圆上异于其顶点的一点,以线段PB为直径的圆经过点F1,经过点F2的直线l与该圆相切,求直线l的斜率.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
(Ⅰ)求椭圆的离心率;
(Ⅱ)设P为椭圆上异于其顶点的一点,以线段PB为直径的圆经过点F1,经过点F2的直线l与该圆相切,求直线l的斜率.
考点:直线与圆锥曲线的关系,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)由椭圆的顶点和截距式方程求出直线AB的方程,化为一般式方程,利用点到直线的距离公式列出方程化简,再由a、b、c的关系求出离心率的值;
(Ⅱ)由(Ⅰ)可得椭圆方程为
+
=1,设P(x0,y0)求出
、
的坐标,由以线段PB为直径的圆经过点F1得:
•
=0,由向量的数量积运算化简,结合点P在椭圆列出方程,求出点P的坐标,再求出圆心坐标和半径,设直线l的方程为y=k(x-c),由直线与圆相切的条件列出方程,求出k的值即可.
(Ⅱ)由(Ⅰ)可得椭圆方程为
| x2 |
| 2c2 |
| y2 |
| c2 |
| F1B |
| F1P |
| F1B |
| F1P |
解答:
解:(Ⅰ)由题意得,A(a,0)、B(0,b),
则直线AB的方程是
+
=1,即bx+ay-ab=0,
因为原点O到直线AB的距离为
b,所以
b=
,
化简得,a2=2b2,
又c2=a2-b2,则c2=b2,所以e=
=
;
(Ⅱ)由(Ⅰ)可得b2=c2,因此椭圆方程为
+
=1,
设P(x0,y0),由F1(-c,0),B(0,c)得,
=(c,c),
=(x0+c,y0),
因为以线段PB为直径的圆经过点F1,所以
•
=0,
即(x0+c)c+y0c=0,又c≠0,故有x0+y0+c=0.①
又点P在椭圆上,则
+
=1,②
由①和②可得3x20+4cx0=0.
而点P不是椭圆的顶点,故x0=-
c.代入①得y0=
c,
即点P的坐标为(-
c,
c),
设圆的圆心为T(x1,y1),则x1=
=-
c,y1=
=
c,
所以该圆的半径r=
=
c,
设直线l的斜率为k,依题意设直线l的方程为y=k(x-c),
由l与圆相切,可得
c=
,
整理得20k2+20k-1=0,解得k=
或k=
.
则直线AB的方程是
| x |
| a |
| y |
| b |
因为原点O到直线AB的距离为
| ||
| 3 |
| ||
| 3 |
| |-ab| | ||
|
化简得,a2=2b2,
又c2=a2-b2,则c2=b2,所以e=
| c |
| a |
| ||
| 2 |
(Ⅱ)由(Ⅰ)可得b2=c2,因此椭圆方程为
| x2 |
| 2c2 |
| y2 |
| c2 |
设P(x0,y0),由F1(-c,0),B(0,c)得,
| F1B |
| F1P |
因为以线段PB为直径的圆经过点F1,所以
| F1B |
| F1P |
即(x0+c)c+y0c=0,又c≠0,故有x0+y0+c=0.①
又点P在椭圆上,则
| x02 |
| 2c2 |
| y02 |
| c2 |
由①和②可得3x20+4cx0=0.
而点P不是椭圆的顶点,故x0=-
| 4 |
| 3 |
| 1 |
| 3 |
即点P的坐标为(-
| 4 |
| 3 |
| 1 |
| 3 |
设圆的圆心为T(x1,y1),则x1=
-
| ||
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| 2 |
| 3 |
所以该圆的半径r=
(-
|
| ||
| 3 |
设直线l的斜率为k,依题意设直线l的方程为y=k(x-c),
由l与圆相切,可得
| ||
| 3 |
|k(-
| ||||
|
整理得20k2+20k-1=0,解得k=
-5+
| ||
| 10 |
-5-
| ||
| 10 |
点评:本题中考查了椭圆与圆的标准方程及其性质、点与椭圆的位置关系、直线与圆相切问题、点到直线的距离公式、中点坐标公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={0,1,2},集合B={0,2,4},则A∪B=( )
| A、{0} |
| B、{2} |
| C、{0,2,4} |
| D、{0,1,2,4} |
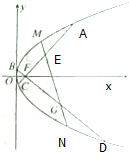 如图,抛物线C:y2=2px(p>0)的焦点F(1,0),过点F任作两条弦AC,BD,且
如图,抛物线C:y2=2px(p>0)的焦点F(1,0),过点F任作两条弦AC,BD,且