Question

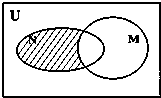已知全集U=R，集合M={x|x＞2}，N={x|

1

2

＜log₂x＜2}，P={x|x≤a-1}．
（1）求如图阴影部分表示的集合；
（2）若N⊆P，求实数a的取值范围．

Answer 1

考点：Venn图表达集合的关系及运算

专题：集合

分析：（1）根据Venn图，得到集合关系为N∩（∁_UM），然后根据集合的基本运算求解即可．
（2）根据集合关系即可得到结论．

解答： 解：（1）由Venn图，得到阴影部分对应的集合为N∩（∁_UM），
∵M={x|x＞2或x＜-2}，
∴（∁_UM）={x|x≤2}，
∵N={x|

1

2

＜log₂x＜2}={x|

2

＜x＜4}，
∴N∩（∁_UM）={x|

2

＜x＜4}∩{x|x≤2}={x|

2

＜x≤2}．
（2）∵N⊆P，∴a-1≥4，即a≥5，
故实数a的取值范围[5，+∞）．

点评：本题主要考查集合的基本运算，利用Venn图确定集合关系是解决本题的关键，比较基础．