题目内容
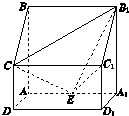 如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.(1)证明:B1C1⊥CE;
(2)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为
| ||
| 6 |
考点:点、线、面间的距离计算
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明CC1⊥B1C1,B1C1⊥C1E,可得B1C1⊥平面CC1E,即可证明结论;
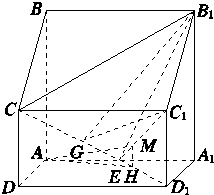
(2)连结D1E,过点M作MH⊥ED1于点H,可得MH⊥平面ADD1A1,连结AH,AM,则∠MAH为直线AM与平面ADD1A1所成的角.设AM=x,求出EH,利用余弦定理建立方程,即可求线段AM的长.
(2)连结D1E,过点M作MH⊥ED1于点H,可得MH⊥平面ADD1A1,连结AH,AM,则∠MAH为直线AM与平面ADD1A1所成的角.设AM=x,求出EH,利用余弦定理建立方程,即可求线段AM的长.
解答:
 (1)证明:因为侧棱CC1⊥平面A1B1C1D1,B1C1?平面A1B1C1D1,
(1)证明:因为侧棱CC1⊥平面A1B1C1D1,B1C1?平面A1B1C1D1,
所以CC1⊥B1C1.
因为AD=CD=1,AA1=AB=2,E为棱AA1的中点,
所以B1E=
,B1C1=
,EC1=
,
从而B1E2=B1C
+EC
,
所以在△B1EC1中,B1C1⊥C1E.
又CC1,C1E?平面CC1E,CC1∩C1E=C1,
所以B1C1⊥平面CC1E,
又CE?平面CC1E,故B1C1⊥CE.
(2)解:连结D1E,过点M作MH⊥ED1于点H,可得MH⊥平面ADD1A1,
连结AH,AM,则∠MAH为直线AM与平面ADD1A1所成的角.
设AM=x,从而在Rt△AHM中,有MH=
x,AH=
x.
在Rt△C1D1E中,C1D1=1,ED1=
,得EH=
MH=
x.
在△AEH中,∠AEH=135°,AE=1,由AH2=AE2+EH2-2AE•EHcos 135°,得
x2=1+
x2+
x.
整理得5x2-2
x-6=0,解得x=
(负值舍去),
所以线段AM的长为
.
 (1)证明:因为侧棱CC1⊥平面A1B1C1D1,B1C1?平面A1B1C1D1,
(1)证明:因为侧棱CC1⊥平面A1B1C1D1,B1C1?平面A1B1C1D1,所以CC1⊥B1C1.
因为AD=CD=1,AA1=AB=2,E为棱AA1的中点,
所以B1E=
| 5 |
| 2 |
| 3 |
从而B1E2=B1C
2 1 |
2 1 |
所以在△B1EC1中,B1C1⊥C1E.
又CC1,C1E?平面CC1E,CC1∩C1E=C1,
所以B1C1⊥平面CC1E,
又CE?平面CC1E,故B1C1⊥CE.
(2)解:连结D1E,过点M作MH⊥ED1于点H,可得MH⊥平面ADD1A1,
连结AH,AM,则∠MAH为直线AM与平面ADD1A1所成的角.
设AM=x,从而在Rt△AHM中,有MH=
| ||
| 6 |
| ||
| 6 |
在Rt△C1D1E中,C1D1=1,ED1=
| 2 |
| 2 |
| 1 |
| 3 |
在△AEH中,∠AEH=135°,AE=1,由AH2=AE2+EH2-2AE•EHcos 135°,得
| 17 |
| 18 |
| 1 |
| 9 |
| ||
| 3 |
整理得5x2-2
| 2 |
| 2 |
所以线段AM的长为
| 2 |
点评:本题考查了直线与平面垂直的性质,考查了线面角和二面角的求法,考查余弦定理,考查小时分析解决问题的能力,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知中心在原点、焦点在x轴上的椭圆C1与双曲线C2有共同的焦点,设左右焦点分别为F1,F2,P是C1与C2在第一象限的交点,△PF1F2是以PF1为底边的等腰三角形,若椭圆与双曲线的离心率分别为e1,e2,则e1•e2的取值范围是( )
A、(
| ||
B、(
| ||
C、(
| ||
| D、(0,+∞) |
已知a>0,b>0,若不等式mab≤(3a+b)(b+3a)恒成立,则m的最大值等于( )
| A、12 | B、9 | C、6 | D、3 |
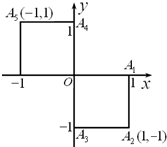 甲、乙、丙三人中要选一人去参加唱歌比赛,于是他们制定了一个规则,规则为:(如图)以O为起点,再从A1,A2,A3,A4,A5,这5个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就让甲去;若X=0就让乙去;若X<0就是丙去.
甲、乙、丙三人中要选一人去参加唱歌比赛,于是他们制定了一个规则,规则为:(如图)以O为起点,再从A1,A2,A3,A4,A5,这5个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就让甲去;若X=0就让乙去;若X<0就是丙去.