题目内容
已知数列{an}中,a1=
,an+1=
(n∈N*).
(Ⅰ)求证:数列{
}是等差数列,并求{an}的通项公式;
(Ⅱ)设bn+an=l(n∈N*),Sn=b1b2+b2b3+…+bnbn+1,试比较an与8Sn的大小.
| 3 |
| 4 |
| 1 |
| 2-an |
(Ⅰ)求证:数列{
| 1 |
| an-1 |
(Ⅱ)设bn+an=l(n∈N*),Sn=b1b2+b2b3+…+bnbn+1,试比较an与8Sn的大小.
考点:数列与不等式的综合,等差关系的确定,数列的求和
专题:等差数列与等比数列
分析:(I)利用已知递推式,只要证明
-
是一个常数即可;
(II)利用“裂项求和”和“作差法”即可得出.
| 1 |
| an+1-1 |
| 1 |
| an-1 |
(II)利用“裂项求和”和“作差法”即可得出.
解答:
解:(Ⅰ)∵an+1=
(n∈N*),
∴
-
=
-
=
-
=-1,
又
=
=-4,
∴数列{
}是首项为-4,公差为-1的等差数列.
∴
=-4-(n-1)=-n-3,化为an=
(n∈N*).
(Ⅱ)∵bn+an=l(n∈N*),
∴bn=1-an=
,
∴bnbn+1=
-
,
∴S=b1b2+b2b3+…+bnbn+1=(
-
)+(
-
)+…+(
-
)=
-
=
,
从而an-8Sn=
-
=
,
∴当n≤2时,an>8Sn;
当n≥3时,an<8Sn.
| 1 |
| 2-an |
∴
| 1 |
| an+1-1 |
| 1 |
| an-1 |
| 1 | ||
|
| 1 |
| an-1 |
| 2-an |
| an-1 |
| 1 |
| an-1 |
又
| 1 |
| a1-1 |
| 1 | ||
|
∴数列{
| 1 |
| an-1 |
∴
| 1 |
| an-1 |
| n+2 |
| n+3 |
(Ⅱ)∵bn+an=l(n∈N*),
∴bn=1-an=
| 1 |
| n+3 |
∴bnbn+1=
| 1 |
| n+3 |
| 1 |
| n+4 |
∴S=b1b2+b2b3+…+bnbn+1=(
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| n+3 |
| 1 |
| n+4 |
| 1 |
| 4 |
| 1 |
| n+4 |
| n |
| 4(n+4) |
从而an-8Sn=
| n+2 |
| n+3 |
| 2n |
| n+4 |
| -n2+8 |
| (n+3)(n+4) |
∴当n≤2时,an>8Sn;
当n≥3时,an<8Sn.
点评:本题考查了递推式的意义、等差数列的定义及其通项公式、“裂项求和”和“作差法”等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
若直线m不平行于平面α,且m?α,则下列结论成立的是( )
| A、α内的所有直线与m异面 |
| B、α内的直线与m都相交 |
| C、α内存在唯一的直线与m平行 |
| D、α内不存在与m平行的直线 |
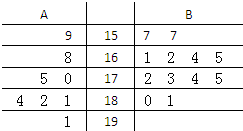 某园艺师培育了两种珍稀树苗A与B,株数分别为8与12,现将这20株树苗的高度编写成如图所示茎叶图(单位:cm).若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.
某园艺师培育了两种珍稀树苗A与B,株数分别为8与12,现将这20株树苗的高度编写成如图所示茎叶图(单位:cm).若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.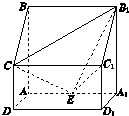 如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.