题目内容
已知a>0,b>0,若不等式mab≤(3a+b)(b+3a)恒成立,则m的最大值等于( )
| A、12 | B、9 | C、6 | D、3 |
考点:基本不等式
专题:不等式的解法及应用
分析:由题意可得m≤
=
,利用基本不等式求得
的最小值,可得m的最大值.
| (3a+b)(b+3a) |
| ab |
| 6ab+9a2+b2 |
| ab |
| 6ab+9a2+b2 |
| ab |
解答:
解:由题意可得m≤
=
≥
=12,
当且仅当9a2=b2,即b=3a时等号成立,
故m的最大值等于12,
故选:A.
| (3a+b)(b+3a) |
| ab |
| 6ab+9a2+b2 |
| ab |
6ab+2
| ||
| ab |
当且仅当9a2=b2,即b=3a时等号成立,
故m的最大值等于12,
故选:A.
点评:本题主要考查基本不等式的应用,函数的恒成立问题,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知∠BAC在平面α内,PA是α的斜线,若∠PAB=∠PAC=∠BAC=60°,PA=a,则点P到平面α的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
(理)y=sin3x+cos2x-sinx的最大值( )
A、
| ||
B、
| ||
C、
| ||
D、
|
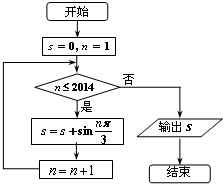
执行如图所示的程序框图,若输入的p=0.8,则输出的n为( )


| A、4 | B、5 | C、6 | D、3 |
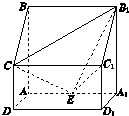 如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.