题目内容
已知数列{an}的各项均为正数,前n项和为Sn,且Sn=
(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=
,Tn=b1+b2+…+bn,求Tn.
| an(an+1) |
| 2 |
(1)求数列{an}的通项公式;
(2)设bn=
| 2Sn |
| (-2)n(n+1) |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)在递推式中取n=1求得a1,然后取n=n-1得另一递推式,作差后整理得到数列{an}为等差数列,则数列的通项公式可求;
(2)把an代入Sn=
,求得Sn后代入bn=
,然后利用错位相减法求得Tn.
(2)把an代入Sn=
| an(an+1) |
| 2 |
| 2Sn |
| (-2)n(n+1) |
解答:
解:(1)Sn=
(n∈N*),
当n=1时,S1=
,∴a1=1,
当n≥2时,
由Sn=
,得2Sn=an2+an ①
取n=n-1,得2Sn-1=an-12+an-1 ②
①-②得:2an=2(Sn-Sn-1)=an2-an-12+an-an-1,
∴(an+an-1)(an-an-1-1)=0,
∵an+an-1>0,
∴an-an-1=1,n≥2,
∴数列{an}是等差数列,
则an=n;
(2)由Sn=
,an=n,
∴Sn=
,
则bn=
=
,
∴Tn=
+
+…+
+
,
-2Tn=1+
+…+
+
,
两式作差得:
∴-3Tn=1+
+…+
-
=
-
=
-
,
∴Tn=
-
=
-
.
| an(an+1) |
| 2 |
当n=1时,S1=
| a1(a1+1) |
| 2 |
当n≥2时,
由Sn=
| an(an+1) |
| 2 |
取n=n-1,得2Sn-1=an-12+an-1 ②
①-②得:2an=2(Sn-Sn-1)=an2-an-12+an-an-1,
∴(an+an-1)(an-an-1-1)=0,
∵an+an-1>0,
∴an-an-1=1,n≥2,
∴数列{an}是等差数列,
则an=n;
(2)由Sn=
| an(an+1) |
| 2 |
∴Sn=
| n(n+1) |
| 2 |
则bn=
| 2Sn |
| (-2)n(n+1) |
| n |
| (-2)n |
∴Tn=
| 1 |
| -2 |
| 2 |
| (-2)2 |
| n-1 |
| (-2)n-1 |
| n |
| (-2)n |
-2Tn=1+
| 2 |
| -2 |
| n-1 |
| (-2)n-2 |
| n |
| (-2)n-1 |
两式作差得:
∴-3Tn=1+
| 1 |
| -2 |
| 1 |
| (-2)n-1 |
| n |
| (-2)n |
=
1-(-
| ||
1-(-
|
| n |
| (-2)n |
2+(-
| ||
| 3 |
| n |
| (-2)n |
∴Tn=
| n |
| 3(-2)n |
2+(-
| ||
| 9 |
| 3n+2 |
| 9(-2)n |
| 2 |
| 9 |
点评:本题考查了数列递推式,考查了等差关系的确定,训练了利用错位相减法求数列的和,是中档题.

练习册系列答案
相关题目
已知实数x、y满足约束条件
,若
=(x,y),
=(3,-1),设z表示向量
在
方向上的投影,则z的取值范围是( )
|
| a |
| b |
| a |
| b |
A、[-
| ||||||||
| B、[-1,6] | ||||||||
C、[-
| ||||||||
D、[-
|
(理)y=sin3x+cos2x-sinx的最大值( )
A、
| ||
B、
| ||
C、
| ||
D、
|
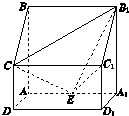 如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.