题目内容
某圆锥体的侧面展开图是半圆,当侧面积是2π时,则该圆锥体的体积是 .
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:由圆锥体侧面展开图的半径是圆锥的母线长,展开图的弧长是底面圆的周长,可以求出圆锥的母线和底面圆半径,从而得出高和体积.
解答:
 解:如图,设侧面展开图半圆的半径为R,侧面面积S侧=
解:如图,设侧面展开图半圆的半径为R,侧面面积S侧=
πR2=2π;
∴R=2.又设圆锥的底面圆半径为r,则2πr=πR,
∴r=
R=1;
∴圆锥的高h=
=
=
;
∴该圆锥体的体积是:V圆锥=
•πr2•h=
•π•12•
=
.
故答案为:
.
 解:如图,设侧面展开图半圆的半径为R,侧面面积S侧=
解:如图,设侧面展开图半圆的半径为R,侧面面积S侧=| 1 |
| 2 |
∴R=2.又设圆锥的底面圆半径为r,则2πr=πR,
∴r=
| 1 |
| 2 |
∴圆锥的高h=
| R2-r2 |
| 22-1 |
| 3 |
∴该圆锥体的体积是:V圆锥=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题通过圆锥体的侧面展开图来求圆锥体的体积,关键是弄清楚侧面展开图与圆锥体的关系是什么.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
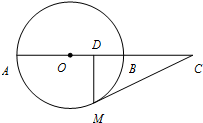 如图,AB为圆O的直径,AB=2,过圆O上一点M作圆O的切线,交AB的延长线于点C,过点M作MD⊥AB于点D,若D是OB中点.则AC•BC=
如图,AB为圆O的直径,AB=2,过圆O上一点M作圆O的切线,交AB的延长线于点C,过点M作MD⊥AB于点D,若D是OB中点.则AC•BC=