题目内容
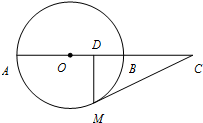如图，AB为圆O的直径，AB=2，过圆O上一点M作圆O的切线，交AB的延长线于点C，过点M作MD⊥AB于点D，若D是OB中点．则AC•BC=考点：与圆有关的比例线段
专题：选作题,立体几何
分析：连接OM，则OM⊥MC，利用射影定理，求出OC，可得AC，BC，即可得出结论．
解答：
解：连接OM，则OM⊥MC，
∵MD⊥AB
∴OM2=OD•OC，
∵AB=2，D是OB中点，
∴OC=2，
∴BC=1，AC=3，
∴AC•BC=3．
故答案为：3．
解：连接OM，则OM⊥MC，∵MD⊥AB
∴OM2=OD•OC，
∵AB=2，D是OB中点，
∴OC=2，
∴BC=1，AC=3，
∴AC•BC=3．
故答案为：3．
点评：本题考查圆的切线的性质，考查射影定理，考查学生的计算能力，属于中档题．
练习册系列答案
小题狂做系列答案
相关题目
