Question

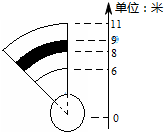如图是一个铅球投掷场地，高二学生A根据平时的检测，他投掷5kg铅球成绩在区间[6，11]（单位：米）内，现在他投掷一次5kg铅球，成绩在区间[8，9]（单位：米）内（图中阴影部分）的概率为（　　）

• A、

  2

  5

• B、

  3

  10

• C、

  π

  5

• D、

  1

  5

Answer 1

考点：几何概型

专题：概率与统计

分析：以面积为测度，分别计算投掷区域的面积，图中阴影部分的面积，再利用几何概型的概率公式，可得结论．

解答： 解：设圆心角为α，则投掷区域的面积为S=

1

2

α•112-

1

2

α•62=

85

2

α，
图中阴影部分的面积为

1

2

α•(92-82)=

17

2

α，
∴成绩在区间[8，9]（单位：米）内（图中阴影部分）的概率为P=

17 2 α

85 2 α

=

1

5

．
故选D．

点评：本题考查几何概型，确定面积为测度是关键．