题目内容
解关于x的不等式ax+
≥a+1(a∈R).
| 1 |
| x |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:将不等式进行“移项,通分”,转化为
≥0,根据各个因式对应根的大小进行分类讨论,分别求解不等式的解集即可得.
| (ax-1)(x-1) |
| x |
解答:
解:∵不等式ax+
≥a+1(a∈R),
∴变形为
≥0,
因式分解可得,
≥0,(*)
①当a=0时,(*)即为
≤0,解得0<x≤1;
②当a≠0时,(*)即为
≥0,
(i)当
<0,即a<0时,解得x≤
或0<x≤1;
(ii)当
≥1,即0<a≤1时,解得0<x≤1或x≥
;
(iii)当
<1,即a>1时,解得0<x≤
或x≥1.
综上所述,当a=0时,原不等式的解集为{x|0<x≤1},
当a<0时,原不等式的解集为{x|x≤
或0<x≤1},
当0<a≤1时,原不等式的解集为{x|0<x≤1或x≥
},
当a>1时,原不等式的解集为{x|0<x≤
或x≥1}
| 1 |
| x |
∴变形为
| ax2-(a+1)x+1 |
| x |
因式分解可得,
| (ax-1)(x-1) |
| x |
①当a=0时,(*)即为
| x-1 |
| x |
②当a≠0时,(*)即为
a(x-
| ||
| x |
(i)当
| 1 |
| a |
| 1 |
| a |
(ii)当
| 1 |
| a |
| 1 |
| a |
(iii)当
| 1 |
| a |
| 1 |
| a |
综上所述,当a=0时,原不等式的解集为{x|0<x≤1},
当a<0时,原不等式的解集为{x|x≤
| 1 |
| a |
当0<a≤1时,原不等式的解集为{x|0<x≤1或x≥
| 1 |
| a |
当a>1时,原不等式的解集为{x|0<x≤
| 1 |
| a |
点评:本题考查了分式不等式的解法,高次不等式的解法.解题的关键是如何进行合理的分类讨论.对于分式不等式,一般是“移项,通分”,将分式不等式转化为各个因式的正负问题.高次不等式一般选用“穿根法”进行求解,“穿根法”要注意先确定各因式的根,在数轴上按照从小到大标出来,确定各因式的系数为正值,根据“奇穿偶不穿”的原则,即可得到不等式的解集.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
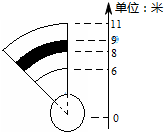 如图是一个铅球投掷场地,高二学生A根据平时的检测,他投掷5kg铅球成绩在区间[6,11](单位:米)内,现在他投掷一次5kg铅球,成绩在区间[8,9](单位:米)内(图中阴影部分)的概率为( )
如图是一个铅球投掷场地,高二学生A根据平时的检测,他投掷5kg铅球成绩在区间[6,11](单位:米)内,现在他投掷一次5kg铅球,成绩在区间[8,9](单位:米)内(图中阴影部分)的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
不等式-x2-5x+6≥0的解集为( )
| A、{x|x≤-6或x≥1} |
| B、{x|x≥6或x≤-1} |
| C、{x|-6≤x≤1} |
| D、{x|-1≤x≤6} |