题目内容
设不等式组
表示的平面区域为D,在区域D内随机取一点P(x0,y0),则点P满足|x|+|y-
|≤
的概率为( )
|
| 2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:几何概型,简单线性规划
专题:概率与统计
分析:确定不等式组表示的区域,求出面积,求出满足|x|+|y-
|≤
在区域D中的区域的面积,利用几何概型概率公式,可得结论.
| 2 |
| 2 |
解答:
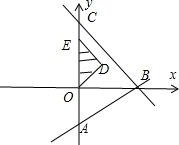 解:不等式组
解:不等式组
表示的平面区域为D,为图中的三角形ABC,其中A(0,-
),B(3,0),C(0,3),其面积为
•(3+
)•3=
,
满足|x|+|y-
|≤
在区域D中的区域为三角形ODE,其中E(0,2
),D(
,
),其面积为
•2
•
=2,
∴所求概率为
=
.
故选C.
 解:不等式组
解:不等式组
|
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 27 |
| 4 |
满足|x|+|y-
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∴所求概率为
| 2 | ||
|
| 8 |
| 27 |
故选C.
点评:本题考查几何概型,考查不等式组表示的平面区域,确定以面积为测度,正确计算面积是关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
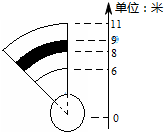 如图是一个铅球投掷场地,高二学生A根据平时的检测,他投掷5kg铅球成绩在区间[6,11](单位:米)内,现在他投掷一次5kg铅球,成绩在区间[8,9](单位:米)内(图中阴影部分)的概率为( )
如图是一个铅球投掷场地,高二学生A根据平时的检测,他投掷5kg铅球成绩在区间[6,11](单位:米)内,现在他投掷一次5kg铅球,成绩在区间[8,9](单位:米)内(图中阴影部分)的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a、b、c分别是角A、B、C的对边,若a2+b2=2014c2,则
的值为( )
| 2tanA•tanB |
| tanC(tanA+tanB) |
| A、0 | B、1 |
| C、2013 | D、2014 |