题目内容
 已知点E(2,1)和圆O:x2+y2=16.
已知点E(2,1)和圆O:x2+y2=16.(Ⅰ)过点E的直线l被圆O所截得的弦长为4
| 3 |
(Ⅱ)试探究是否存在这样的点M:M是圆O内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEM的面积S△OEM=2?若存在,求出点M的坐标,若不存在,说明理由.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(Ⅰ)分类讨论,设出直线方程,利用直线l被圆O所截得的弦长,求出斜率,即可得出直线的方程;
(Ⅱ)连结OE,点A(-4,0),B(4,0)满足S△OEA=S△OEB=2,分别过A、B作直线OE的两条平行线l1、l2,利用M是圆O内部的整点,即可求得结论.
(Ⅱ)连结OE,点A(-4,0),B(4,0)满足S△OEA=S△OEB=2,分别过A、B作直线OE的两条平行线l1、l2,利用M是圆O内部的整点,即可求得结论.
解答:
 解:(Ⅰ)当直线的斜率不存在时,直线的方程为x=2,满足直线l被圆O所截得的弦长为4
解:(Ⅰ)当直线的斜率不存在时,直线的方程为x=2,满足直线l被圆O所截得的弦长为4
;
当直线的斜率存在时,设直线的方程为y-1=k(x-2),
即kx-y-2k+1=0.
∵过点E的直线l被圆O所截得的弦长为4
,
∴圆心到直线的距离为2,∴
=2,
∴k=-
,∴直线的方程为3x+4y-10=0.
综上,所求方程为:x=2或3x+4y-10=0.
(Ⅱ)连结OE,点A(-4,0),B(4,0)满足S△OEA=S△OEB=2,分别过A、B作直线OE的两条平行线l1、l2.
∵kOE=
,∴直线l1、l2的方程分别为:y=
(x+4)、y=
(x-4)
设点M(x,y)(x,y∈Z),则x2+y2<16.
分别解
与
,得-4<x<2
与-2
<x<4
∵x,y∈Z,∴x为偶数,在(-4,2
)上x=-2,0,2对应的y=1,2,3;
在(-2
,4)上x=-2,0,2,对应的y=-3,-2,-1,
∴满足条件的点M存在,共有6个,它们的坐标分别为:(-2,1),(0,2),(2,3),(-2,-3),(0,-2),(2,-1).
 解:(Ⅰ)当直线的斜率不存在时,直线的方程为x=2,满足直线l被圆O所截得的弦长为4
解:(Ⅰ)当直线的斜率不存在时,直线的方程为x=2,满足直线l被圆O所截得的弦长为4| 3 |
当直线的斜率存在时,设直线的方程为y-1=k(x-2),
即kx-y-2k+1=0.
∵过点E的直线l被圆O所截得的弦长为4
| 3 |
∴圆心到直线的距离为2,∴
| |-2k+1| | ||
|
∴k=-
| 3 |
| 4 |
综上,所求方程为:x=2或3x+4y-10=0.
(Ⅱ)连结OE,点A(-4,0),B(4,0)满足S△OEA=S△OEB=2,分别过A、B作直线OE的两条平行线l1、l2.
∵kOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
设点M(x,y)(x,y∈Z),则x2+y2<16.
分别解
|
|
| 2 |
| 5 |
| 2 |
| 5 |
∵x,y∈Z,∴x为偶数,在(-4,2
| 2 |
| 5 |
在(-2
| 2 |
| 5 |
∴满足条件的点M存在,共有6个,它们的坐标分别为:(-2,1),(0,2),(2,3),(-2,-3),(0,-2),(2,-1).
点评:本题考查直线与圆的位置关系,考查存在性问题的研究,考查学生分析解决问题的能力,考查分类讨论是数学思想,有一定的难度.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
变量x,y满足条件
且z=5y-x最大值为a,最小值为b,则a+b值为( )
|
| A、8 | B、-8 | C、16 | D、24 |

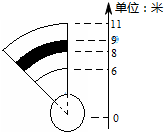 如图是一个铅球投掷场地,高二学生A根据平时的检测,他投掷5kg铅球成绩在区间[6,11](单位:米)内,现在他投掷一次5kg铅球,成绩在区间[8,9](单位:米)内(图中阴影部分)的概率为( )
如图是一个铅球投掷场地,高二学生A根据平时的检测,他投掷5kg铅球成绩在区间[6,11](单位:米)内,现在他投掷一次5kg铅球,成绩在区间[8,9](单位:米)内(图中阴影部分)的概率为( )