题目内容
若实数a,b满足a2+b2≤1,则关于x的方程x2-2x+a+b=0有实数根的概率是 .
考点:几何概型
专题:概率与统计
分析:以a为横坐标、b为纵坐标建立直角坐标系,可得满足a2+b2≤1的点(a,b)在单位圆及其内部;若关于x的方程x2-2x+a+b=0有实数根,则点(a,b)满足a+b≤1,即在单位圆内且直线a+b=1的下方.由此结合几何概型计算公式,用图中黄色阴影部分的面积除以单位圆的面积,即可得到所求的概率.
解答:
 解:以a为横坐标、b为纵坐标建立直角坐标系,
解:以a为横坐标、b为纵坐标建立直角坐标系,
∵实数a,b满足a2+b2≤1,
∴可得所有的点(a,b)在以O为圆心,半径为1的圆及其内部,即单位圆及其内部,如图所示,面积为S=π×12=π
若关于x的方程x2-2x+a+b=0有实数根,则满足△=4-4(a+b)≥0,解之得a+b≤1
符合上式的点(a,b)在圆内且在直线a+b=1的下方,其面积为
π•12+
•1•1=
π+
,
∴关于x的方程x2-2x+a+b=0有实数根的概率是
=
.
故答案为:
.
 解:以a为横坐标、b为纵坐标建立直角坐标系,
解:以a为横坐标、b为纵坐标建立直角坐标系,∵实数a,b满足a2+b2≤1,
∴可得所有的点(a,b)在以O为圆心,半径为1的圆及其内部,即单位圆及其内部,如图所示,面积为S=π×12=π
若关于x的方程x2-2x+a+b=0有实数根,则满足△=4-4(a+b)≥0,解之得a+b≤1
符合上式的点(a,b)在圆内且在直线a+b=1的下方,其面积为
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
∴关于x的方程x2-2x+a+b=0有实数根的概率是
| ||||
| π |
| 3π+2 |
| 4π |
故答案为:
| 3π+2 |
| 4π |
点评:本题几何概型计算公式,考查了弓形面积计算公式、一元二次方程根的判别式,考查学生的计算能力,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
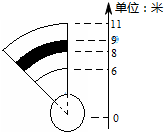 如图是一个铅球投掷场地,高二学生A根据平时的检测,他投掷5kg铅球成绩在区间[6,11](单位:米)内,现在他投掷一次5kg铅球,成绩在区间[8,9](单位:米)内(图中阴影部分)的概率为( )
如图是一个铅球投掷场地,高二学生A根据平时的检测,他投掷5kg铅球成绩在区间[6,11](单位:米)内,现在他投掷一次5kg铅球,成绩在区间[8,9](单位:米)内(图中阴影部分)的概率为( )