题目内容

10．（1）如图1，AB∥CD，AB∩α=E，CD∩α=F，求作BC与平面α的交点O
（2）如图2，3正方体ABCD-A1B1C1D1
（a）过B，C1，D1作正方体的截面；
（b）过C，D1，M作正方体的截面．

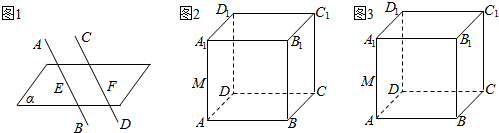
分析 由已知条件，根据题意能求出BC与平面α的交点O、过B，C1，D1作正方体的截面和过C，D1，M作正方体的截面．

解答 解：（1）如图，连结EF，连结BC，交EF于O，则O即为BC与平面α的交点．

（2）连结BD1，BC1，则△BD1C1为过B，C1，D1作出的正方体的截面．

（3）连结MD1，MC，D1C，则△D1MC是过C，D1，M作出的正方体的截面．

点评 本题考查线面交点的作法、考查正方体的截面的作法，是基础，解题地要认真审题，注意基本知识、基本技能的培养．

练习册系列答案
相关题目
20．已知两个非零平面向量$\overrightarrow{a}$，$\overrightarrow{b}$满足：对任意λ∈R恒有|$\overrightarrow{a}$-$λ\overrightarrow{b}$|≥|$\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$|，则：
①若|$\overrightarrow{b}$|=8，则$\overrightarrow{a}•\overrightarrow{b}$=32；
②若$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为$\frac{π}{6}$，则$\frac{|2\overrightarrow{a}+t•\overrightarrow{b}|}{|\overrightarrow{b}|}$的最小值为$\frac{\sqrt{3}}{3}$．
1．已知sin（θ-$\frac{3}{2}π$）+cos（$\frac{3}{2}π+θ$）=$\frac{3}{5}$，求sin3（$\frac{π}{2}$+θ）-cos3（$\frac{3π}{2}$-θ）的值．
18．已知函数y=2sin2x+mcosx-$\frac{1}{8}$．
（1）当m=-1且-$\frac{π}{3}$≤x≤$\frac{2π}{3}$时，求函数值域；
（2）当x∈R时，试讨论函数最大值．
5．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}（x∈[0，+∞））}\\{{a}^{x}+{a}^{2}-3a+1（x∈（-∞，0））}\end{array}\right.$在区间（-∞，+∞）是增函数，则常数a的取值范围是（　　）
A．1≤a≤2B．a＜1或a≥2C．1＜a≤2D．a＜1或a＞2
15．把4个元素的集合划分为2个非空集，其中分为两个个数相同的集合的概率为$\frac{3}{7}$．
2．在平面直角坐标系中，已知动点P到点F1（-4，0）的距离比到点F2（4，0）的距离大6．求：
（1）动点P的轨迹方程；
（2）过点F2且垂直于x轴的直线与点p的轨迹交于A，B两点，求线段AB的长度．
19．已知角α的终边经过点P（x，-$\sqrt{2}$）（x≠0），且cosα=$\frac{\sqrt{3}}{6}$x，求sinα+$\frac{cosα}{sinα}$的值．
10．袋中有大小相同4个小球，编号分别为1，2，3，4，从袋中任取两个球（不放回），则这两个球编号正好相差1的概率是（　　）
A．$\frac{1}{3}$B．$\frac{1}{2}$C．$\frac{2}{3}$D．$\frac{3}{4}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网