题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}{{4}^{x},x>0}\\{f(x+1)-1,x<0}\end{array}\right.$,则f(-$\frac{1}{2}$)+f($\frac{1}{2}$)=( )| A. | 3 | B. | 5 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
分析 利用分段函数的性质求解.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{{4}^{x},x>0}\\{f(x+1)-1,x<0}\end{array}\right.$,
∴f(-$\frac{1}{2}$)=f($\frac{1}{2}$)-1=${4}^{\frac{1}{2}}$-1=1,
f($\frac{1}{2}$)=${4}^{\frac{1}{2}}$=2,
∴f(-$\frac{1}{2}$)+f($\frac{1}{2}$)=1+2=3.
故选:A.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意分段函数的性质的合理运用.

练习册系列答案
相关题目
10.袋中有大小相同4个小球,编号分别为1,2,3,4,从袋中任取两个球(不放回),则这两个球编号正好相差1的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
8.命题“?x∈R,使得x2<1”的否定是( )
| A. | ?x∈R,都有x2<1 | B. | ?x∈R,使得x2≥1 | C. | ?x∈R,都有x2≥1 | D. | ?x∈R,使得x2>1 |
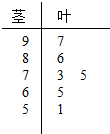 北京高中会考考试科目原始得分采用百分制,公布成绩使用A、B、C、D等级制.A、B、C三级为合格等级,D为不合格等级.各等级分数划分标准:85分及以上为A,84-70分为B,69-60分为C,60分以下为D.如图的茎叶图(十位为茎,个位为叶)记录了某校高三年级6名学生的数学会考成绩.
北京高中会考考试科目原始得分采用百分制,公布成绩使用A、B、C、D等级制.A、B、C三级为合格等级,D为不合格等级.各等级分数划分标准:85分及以上为A,84-70分为B,69-60分为C,60分以下为D.如图的茎叶图(十位为茎,个位为叶)记录了某校高三年级6名学生的数学会考成绩. 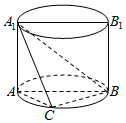 如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.
如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.