题目内容
相交成90°的两条直线与一个平面所成的角分别是30°与45°,则这两条直线在该平面内的射影所成角的正弦值为 .
考点:空间中直线与平面之间的位置关系
专题:空间角
分析:已知PA⊥PB,PO⊥平面AOB,∠PAO=30°,∠PBO=45°,直线PA,PB这两条直线在该平面内的射影所成角为∠AOB,由此能求出这两条直线在该平面内的射影所成角的正弦值.
解答:
解:如图,已知PA⊥PB,PO⊥平面AOB,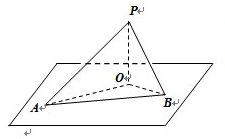
∠PAO=30°,∠PBO=45°,
直线PA,PB这两条直线在该平面内的射影所成角为∠AOB,
设PO=x,则AO=
x,BO=x,PA=
=2x,PB=
=
x,
AB=
=
x,
∴cos∠AOB=
=-
,
∴sin∠AOB=
=
.
∴这两条直线在该平面内的射影所成角的正弦值为
.
故答案为:
.

∠PAO=30°,∠PBO=45°,
直线PA,PB这两条直线在该平面内的射影所成角为∠AOB,
设PO=x,则AO=
| 3 |
| PO2+AO2 |
| PO2+BO2 |
| 2 |
AB=
| PA2+PB2 |
| 6 |
∴cos∠AOB=
| AO2+BO2-AB2 |
| 2AO•BO |
| ||
| 3 |
∴sin∠AOB=
1-(-
|
| ||
| 3 |
∴这两条直线在该平面内的射影所成角的正弦值为
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查两条直线在平面内的射影所成角的正弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知圆x2+y2=4与圆x2+y2-2y-6=0,则两圆的公共弦长为( )
A、
| ||
B、2
| ||
| C、2 | ||
| D、1 |
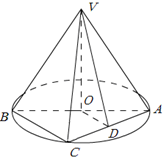 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.
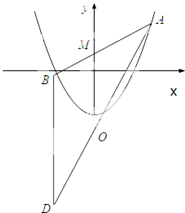 如图,已知抛线C:x2=4y,过点M(0,2)任作一直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).
如图,已知抛线C:x2=4y,过点M(0,2)任作一直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点). 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为EC中点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为EC中点.