题目内容
已知数列{an}的首项a1=
,an+1=
,请证明a1+a2+…+an>
(用数学归纳法)
| 3 |
| 5 |
| 3an |
| 2an+1 |
| n2 |
| n+1 |
考点:数学归纳法,数列的求和
专题:点列、递归数列与数学归纳法
分析:由an+1=
,得
=
+
,即
-1=
(
-1),又
-1=
-1=
,故(
-1)是以
为首项,
为公比的等比数列.求得an=
,再利用数学归纳法即可证明.
| 3an |
| 2an+1 |
| 1 |
| an+1 |
| 2 |
| 3 |
| 1 |
| 3an |
| 1 |
| an+1 |
| 1 |
| 3 |
| 1 |
| an |
| 1 |
| a1 |
| 5 |
| 3 |
| 2 |
| 3 |
| 1 |
| an |
| 2 |
| 3 |
| 1 |
| 3 |
| 3n |
| 3n+2 |
解答:
解:∵an+1=
,∴
=
+
,
∴
-1=
(
-1),又
-1=
-1=
,
∴(
-1)是以
为首项,
为公比的等比数列.
∴
-1=
•
=
,
∴an=
,
用数学归纳法证明如下:
①当n=1时,由题意可知,左边=a1=
,右边=
,命题成立,
②假设当n=k(k≥1,k∈N)时命题成立,即a1+a2+…+ak>
,
那么,当n=k+1时,a1+a2+…+ak+ak+1>
+
>
,也就说,当n=k+1时命题也成立,
综上所述,a1+a2+…+an>
.
| 3an |
| 2an+1 |
| 1 |
| an+1 |
| 2 |
| 3 |
| 1 |
| 3an |
∴
| 1 |
| an+1 |
| 1 |
| 3 |
| 1 |
| an |
| 1 |
| a1 |
| 5 |
| 3 |
| 2 |
| 3 |
∴(
| 1 |
| an |
| 2 |
| 3 |
| 1 |
| 3 |
∴
| 1 |
| an |
| 2 |
| 3 |
| 1 |
| 3n-1 |
| 2 |
| 3n |
∴an=
| 3n |
| 3n+2 |
用数学归纳法证明如下:
①当n=1时,由题意可知,左边=a1=
| 3 |
| 5 |
| 1 |
| 2 |
②假设当n=k(k≥1,k∈N)时命题成立,即a1+a2+…+ak>
| k2 |
| k+1 |
那么,当n=k+1时,a1+a2+…+ak+ak+1>
| k2 |
| k+1 |
| 3k+1 |
| 3k+1+2 |
| (k+1)2 |
| (k+1)+1 |
综上所述,a1+a2+…+an>
| n2 |
| n+1 |
点评:本题考查数列递推式,考查数列的通项,考查数学归纳法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
给出如图所示程序:执行该程序时,若输入x为4,则输出y值为( )


| A、3 | B、8 | C、9 | D、64 |
 在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.
在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.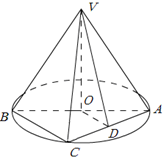 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.