题目内容
两个等差数列的前n项和之比为
，则它们的第7项之比为 ．
| 5n+10 |
| 2n-1 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：两个等差数列的第n项的比等于这两个等差数列的前2n-1项和的比．
解答：
解：设这两个等差数列的前n项和分别为Sn，Tn，
由题意知
=
=
=3，
故答案为：3：1
由题意知
| a7 |
| b7 |
| S13 |
| T13 |
| 75 |
| 25 |
故答案为：3：1
点评：本题考查等差数列的性质和应用，解题时要注意公式的灵活运用．
练习册系列答案
字词句段篇系列答案
相关题目
已知集合P={x|x=m2+1，m∈N*}，Q={x|x=n2-4n+5，n∈N*}，则（ ）
| A、P=Q | B、P?Q |
| C、Q?P | D、以上皆错 |
下列给出的赋值语句中正确的是（ ）
| A、x=3 | B、3=x |
| C、x-3=0 | D、3-x=0 |
若指数函数f（x）=ax是R上的减函数，则a的取值范围是（ ）
| A、a＞0 | B、a＜0 |
| C、0＜a＜1 | D、a＞1 |
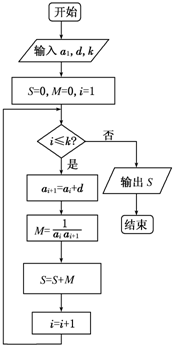已知等差数列{an}的各项均为正数，观察如图所示的程序框图，当k=5，k=10时，分别有S=| 5 |
| 11 |
| 10 |
| 21 |
| A、an=2n+1 |
| B、an=2n+3 |
| C、an=2n-1 |
| D、an=2n-3 |