题目内容
5.函数f(x)=x2(x-$\frac{2}{x}$)的导数为f′(x),则f′(1)等于( )| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
分析 利用导数的运算法则可得f′(x),即可得出.
解答 解:f(x)=x2(x-$\frac{2}{x}$)=x3-2x,
f′(x)=3x2-2,
∴f′(1)=3-2=1.
故选:A.
点评 本题考查了导数的运算法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.空间直角坐标系中,点A(-2,1,3)关于点B(1,-1,2)的对称点C的坐标为( )
| A. | (4,1,1) | B. | (-1,0,5) | C. | (4,-3,1) | D. | (-5,3,4) |
16.在正三棱柱ABC-A1B1C1中,已知AB=2,CC1=$\sqrt{2}$,则异面直线AB1和BC1所成角的余弦值为( )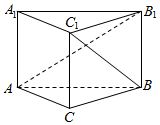

| A. | 0 | B. | $\frac{\sqrt{42}}{7}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
10.下列选项中,说法正确的是( )
| A. | 已知命题p和q,若“p∨q”为假命题,则命题p和q中必一真一假 | |
| B. | 命题“?c∈R,方程2x2+y2=c表示椭圆”的否定是“?c∈R,方程2x2+y2=c不表示椭圆” | |
| C. | 命题“若k<9,则方程“$\frac{x^2}{25-k}$+$\frac{y^2}{k-9}$=1表示双曲线”是假命题 | |
| D. | 命题“在△ABC中,若sinA<$\frac{1}{2}$,则A<$\frac{π}{6}$”的逆否命题为真命题 |
14.F为双曲线Г:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,若Г上存在一点P使得△OPF为等边三角形(O为坐标原点),则Г的离心率e为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\sqrt{3}+1$ | D. | 2 |
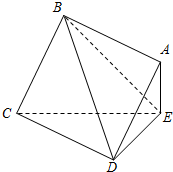 如图,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,
如图,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD, 如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为( )
如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为( )