题目内容
10.下列选项中,说法正确的是( )| A. | 已知命题p和q,若“p∨q”为假命题,则命题p和q中必一真一假 | |
| B. | 命题“?c∈R,方程2x2+y2=c表示椭圆”的否定是“?c∈R,方程2x2+y2=c不表示椭圆” | |
| C. | 命题“若k<9,则方程“$\frac{x^2}{25-k}$+$\frac{y^2}{k-9}$=1表示双曲线”是假命题 | |
| D. | 命题“在△ABC中,若sinA<$\frac{1}{2}$,则A<$\frac{π}{6}$”的逆否命题为真命题 |
分析 分别判断各个选项的正误,从而求出答案.
解答 解:对于A:若“p∨q”为假命题,则命题p和q均是假命题,故A错误;
对于B:命题“?c∈R,方程2x2+y2=c表示椭圆”的否定是“?c∈R,方程2x2+y2=c不表示椭圆,故B正确;
对于C:命题“若k<9,则方程“$\frac{x^2}{25-k}$+$\frac{y^2}{k-9}$=1表示双曲线”是真命题,故C错误;
对于D:命题“在△ABC中,若sinA<$\frac{1}{2}$,则A<$\frac{π}{6}$”是假命题,故其逆否命题为假命题,故D错误;
故选:B.
点评 本题考查了充分必要条件,考查四种命题的关系,考查椭圆、双曲线以及三角函数问题,是一道基础题.

练习册系列答案
相关题目
20.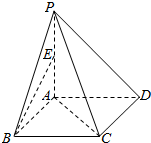 四棱锥P-ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=2,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是( )
四棱锥P-ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=2,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是( )
 四棱锥P-ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=2,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是( )
四棱锥P-ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=2,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是( )| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
1.已知点A(0,0,0),B(1,0,1),C(0,1,1),则平面ABC的一个法向量$\overrightarrow m$是( )
| A. | (1,1,1) | B. | (1,1,-1) | C. | (-1,1,1) | D. | (1,-1,1) |
18.设奇函数f(x)在(0,+∞)上为增函数,且$f({\sqrt{3}})=0$,则不等式x[f(x)-f(-x)]<0的解集为( )
| A. | $({-\sqrt{3},0})∪({\sqrt{3},+∞})$ | B. | $({-\sqrt{3},0})∪({0,\sqrt{3}})$ | C. | $({-∞,-\sqrt{3}})∪({0,\sqrt{3}})$ | D. | $({-∞,-\sqrt{3}})∪({\sqrt{3},+∞})$ |
5.函数f(x)=x2(x-$\frac{2}{x}$)的导数为f′(x),则f′(1)等于( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |