题目内容
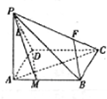 如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA⊥平面ABCD,AB=
如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA⊥平面ABCD,AB=| 3 |
(1)M是AB上一点,且AM=
| ||
| 3 |
| PF |
| FC |
(2)E为PD的中点,在侧面PAB内找一点N,使NE⊥平面PAC,并求NE与平面PAD所成角的大小.
考点:直线与平面所成的角,直线与平面平行的判定
专题:圆锥曲线中的最值与范围问题
分析:(1)当
=2时,BF∥平面PDM.F作FG∥PD,交CD于G,则CG=
GD,连结BG,得四边形BMDG这平行四边形,由此能证明BF∥平面PDM.
(2)建立空间直角坐标系,利用向量法能求出NE与平面PAD所成角.
| PF |
| FC |
| 1 |
| 2 |
(2)建立空间直角坐标系,利用向量法能求出NE与平面PAD所成角.
解答:
解:(1)当
=2时,BF∥平面PDM.
证明如下:
F作FG∥PD,交CD于G,则CG=
GD,连结BG,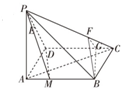
∵AB
CD,AM=
MB,
∴BM
DC,即四边形BMDG这平行四边形,∴BG∥DM,
∴平面BFG∥平面PDM,
∵BF?平面BFG,∴BF∥平面PDM.
(2)建立如图所示的空间直角坐标系,
则A(0,0,0),C(
,1,0),D(0,1,0),P(0,0,2),E(0,
,1),
则
=(0,0,2),
=(
,1,0),
由于N点在侧面PAB内,
故设N(x,z),则
=(-x,
,1-z),
由NE⊥平面PAC,得
,
∴
=(-
,
,0),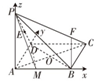
∵平面PAD的一个法向量
=(1,0,0),
∴|cos<
,
>|=
=
,
设NE与平面PAD所成角为θ,
则sinθ=
,∴θ=
,
∴NE与平面PAD所成角为
.
| PF |
| FC |
证明如下:
F作FG∥PD,交CD于G,则CG=
| 1 |
| 2 |

∵AB
| ∥ |
. |
| 1 |
| 2 |
∴BM
| ∥ |
. |
∴平面BFG∥平面PDM,
∵BF?平面BFG,∴BF∥平面PDM.
(2)建立如图所示的空间直角坐标系,
则A(0,0,0),C(
| 3 |
| 1 |
| 2 |
则
| AP |
| AC |
| 3 |
由于N点在侧面PAB内,
故设N(x,z),则
| NE |
| 1 |
| 2 |
由NE⊥平面PAC,得
|
∴
| NE |
| ||
| 6 |
| 1 |
| 2 |

∵平面PAD的一个法向量
| n |
∴|cos<
| NE |
| n |
|-
| ||||
|
| 1 |
| 2 |
设NE与平面PAD所成角为θ,
则sinθ=
| 1 |
| 2 |
| π |
| 6 |
∴NE与平面PAD所成角为
| π |
| 6 |
点评:本题考查直线与平面平行的证明,考查直线与平面所成的角的大小,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25),{25,30),[30,35),[35,40)[40,45].
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25),{25,30),[30,35),[35,40)[40,45].