题目内容
在△ABC中，三内角A、B、C的对边分别是a、b、c，其中c=10，
=
=-
．
（1）判断△ABC的形状；
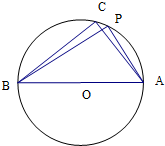
（2）若△ABC外接圆为⊙O，点P位于劣弧
上，∠APB=60°，求四边形ABCP的面积．
| sin(A-B) |
| sin(A+B) |
| a2-b2 |
| a2+b2 |
| 7 |
| 25 |
（1）判断△ABC的形状；
（2）若△ABC外接圆为⊙O，点P位于劣弧
 |
| AC |
考点：两角和与差的正弦函数,正弦定理
专题：解三角形
分析：（1）根据正弦定理将条件进行化简即可判断△ABC的形状；
（2）根据两角和与差的三角公式，即可求四边形ABCP的面积．
（2）根据两角和与差的三角公式，即可求四边形ABCP的面积．
解答：
解：（1）∵
=
，
∴（a2+b2）sin（A-B）=（a2-b2）sin（A+B），
即b2sinAcosB=a2cosAsinB，
由正弦定理得sin2BsinAcosB=sin2AcosAsinB，
∴sinBcosB=sinAcosA，即sin2A=sin2B，
则2A=2B或2A=π-2B，
即A=B或A+B=
，
∵
=-
≠0，
∴a≠b，
故A+B=
，
∴△ABC为直角三角形；
（2）∵
=-
，c=10，
∴a2+b2=100，
即a2-b2=-28，
解得a=6，b=8，
则Rt△ABC中，sin∠CAB=
，cos∠CAB=
，
sin∠PAC=sin（60°-∠CAB）=sin60°cos∠CAB-cos60°sin∠CAB=
，
连BP，CP，则AP=ABcos60°=5，
则四边形ABCP的面积S=S△ABC+S△PBC=
ab+
AP•ACsin∠PAC=18+8
．
解：（1）∵| sin(A-B) |
| sin(A+B) |
| a2-b2 |
| a2+b2 |
∴（a2+b2）sin（A-B）=（a2-b2）sin（A+B），
即b2sinAcosB=a2cosAsinB，
由正弦定理得sin2BsinAcosB=sin2AcosAsinB，
∴sinBcosB=sinAcosA，即sin2A=sin2B，
则2A=2B或2A=π-2B，
即A=B或A+B=
| π |
| 2 |
∵
| a2-b2 |
| a2+b2 |
| 7 |
| 25 |
∴a≠b，
故A+B=
| π |
| 2 |
∴△ABC为直角三角形；
（2）∵
| a2-b2 |
| a2+b2 |
| 7 |
| 25 |
∴a2+b2=100，
即a2-b2=-28，
解得a=6，b=8，
则Rt△ABC中，sin∠CAB=
| 3 |
| 5 |
| 4 |
| 5 |
sin∠PAC=sin（60°-∠CAB）=sin60°cos∠CAB-cos60°sin∠CAB=
4
| ||
| 10 |
连BP，CP，则AP=ABcos60°=5，
则四边形ABCP的面积S=S△ABC+S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
点评：本题主要考查三角形形状的判断，以及正弦定理的应用，综合考查了三角函数的公式的应用，
练习册系列答案
开心蛙口算题卡系列答案
相关题目
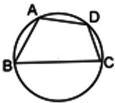为了提高校园景观，某校改造花圃用地平面示意图如图所示，经规划调研确定，花圃规划用地区域近似地为半径是R的圆面．该圆面的内接四边形ABCD是原花圃用地，测量可知边界AB=AD=4米，BC=6米，CD=2米．