题目内容
6.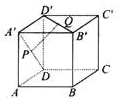 如图,在正方体ABCD-A′B′C′D′中,P是A′D的中点,Q是B′D′的中点,判断直线PQ与平面AA′B′B的位置关系,并利用定义证明.
如图,在正方体ABCD-A′B′C′D′中,P是A′D的中点,Q是B′D′的中点,判断直线PQ与平面AA′B′B的位置关系,并利用定义证明.
分析 直线与平面的关系,转化为平面与平面的关系;P是A′D的中点,Q是B′D′的中点,作A′D′的中点为N.可得平面AA′B′B与平面PQN的关系,判断直线PQ与平面AA′B′B的位置关系.
解答 解:直线PQ与平面AA′B′B平行.
证明:∵P是A′D的中点,Q是B′D′的中点,作A′D′的中点为N.
连接PN,QN,可得:PN∥A′A,QN∥A′B′,
A′A∩A′B′=A′,PN、QN?平面PQN,A′A、A′B′?平面AA′B′B
∴平面AA′B′B与平面PQN平行.
∵PQ?平面PQN
故得直线PQ与平面AA′B′B平行.
点评 本题考查了直线与平面的关系,转化为平面与平面的关系来证明.比较基础.

练习册系列答案
相关题目
1.在复平面内,复数z的对应点为(1,1),则$\frac{2}{z}$-z2=( )
| A. | -1-3i | B. | -1+3i | C. | 1-3i | D. | 1+3i |
11.满足{-1,0,1}?M⊆{-1,0,1,2,3,4}的集合M的个数是( )
| A. | 4个 | B. | 6个 | C. | 7个 | D. | 8个 |
18.已知抛物线的焦点坐标为(-$\frac{1}{32}$,0),则抛物线的标准方程为( )
| A. | x=-8y2 | B. | y=-8x2 | C. | x=-16y2 | D. | y=-16x2 |
15.已知椭圆$\frac{x^2}{16}+\frac{y^2}{9}$=1,直线l:y=kx+t(k为常数,t≠0)与椭圆相交于A,B两点,记△AOB的面积为S(其中O为坐标原点),则函数S=f(t)的奇偶性为( )
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 非奇非偶函数 | D. | 奇偶性与k的值有关 |
16.已知f(x)是定义在R上的奇函数,且在(0,+∞)是增函数,又f(-3)=0,则不等式x•f(x)≥0的解集是( )
| A. | {x|-3≤x≤3} | B. | {x|-3≤x<0或0<x≤3} | C. | {x|x≤-3或x≥3} | D. | {x|x≤-3或x=0或x≥3} |