题目内容
17.函数y=$\frac{{{e^x}•{x^2}}}{{{e^{2x}}-1}}$的大致图象是( )| A. |  | B. | 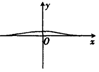 | C. |  | D. |  |
分析 根据函数在x=0时,解析式无意义,可得函数图象与y轴无交点,利用排除法,可得答案.
解答 解:当x=0时,解析式的分母为0,解析式无意义,
故函数图象与y轴无交点,
故排除A,B,D,
故选:C
点评 本题考查的知识点是函数的图象,排除法是解答此类问题的常用方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.若$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是平面内的一组基底,则下列四组向量不能作为平面向量的基底的是( )
| A. | $\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$和$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$ | B. | 3$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$和-6$\overrightarrow{{e}_{1}}$+4$\overrightarrow{{e}_{2}}$ | ||
| C. | $\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$和2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$ | D. | $\overrightarrow{{e}_{2}}$和$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$ |
7.下面四组函数中,f(x)与g(x)表示同一个函数的是( )
| A. | f(x)=|x|,$g(x)={({\sqrt{x}})^2}$ | B. | f(x)=2x,$g(x)=\frac{{2{x^2}}}{x}$ | C. | f(x)=x,$g(x)=\root{3}{x^3}$ | D. | f(x)=x,$g(x)=\frac{1}{{\sqrt{x^2}}}$ |
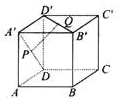 如图,在正方体ABCD-A′B′C′D′中,P是A′D的中点,Q是B′D′的中点,判断直线PQ与平面AA′B′B的位置关系,并利用定义证明.
如图,在正方体ABCD-A′B′C′D′中,P是A′D的中点,Q是B′D′的中点,判断直线PQ与平面AA′B′B的位置关系,并利用定义证明.