题目内容
已知数列{an}中,Sn为前n项的和,2Sn=3an-1.
(Ⅰ)求an;
(Ⅱ)若数列{bn}满足bn=an+(-1)nlog3an,求数列{bn}的前2n项和T2n.
(Ⅰ)求an;
(Ⅱ)若数列{bn}满足bn=an+(-1)nlog3an,求数列{bn}的前2n项和T2n.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)根据条件建立方程组,得到数列{an}是等比数列,即可求an;
(Ⅱ)利用分组求和法,即可求出数列的前2n项和.
(Ⅱ)利用分组求和法,即可求出数列的前2n项和.
解答:
解:(Ⅰ)因为2Sn=3an-1,
所以2Sn-1=3an-1-1,(n≥2)
两式相减得2an=3an-3an-1,
所以 an=3an-1,
所以数列{an}是等比数列的公比q=3
当n=1,得2a1=3a1-1,解得a1=1.
则an=3n-1.
(Ⅱ) bn=an+(-1)nlog3an=3n-1+(-1)nlog33n-1=3n-1+(-1)n(n-1),
则数列{bn}的前2n项和T2n=(1+3+32+…+32n-1)+[-0+1-2+3-…+(2n-1)]=
+n=
+n-
.
所以2Sn-1=3an-1-1,(n≥2)
两式相减得2an=3an-3an-1,
所以 an=3an-1,
所以数列{an}是等比数列的公比q=3
当n=1,得2a1=3a1-1,解得a1=1.
则an=3n-1.
(Ⅱ) bn=an+(-1)nlog3an=3n-1+(-1)nlog33n-1=3n-1+(-1)n(n-1),
则数列{bn}的前2n项和T2n=(1+3+32+…+32n-1)+[-0+1-2+3-…+(2n-1)]=
| 1-32n |
| 1-3 |
| 32n |
| 2 |
| 1 |
| 2 |
点评:本题主要考查数列的通项公式的求解以及数列求和,利用分组求和法以及等差数列和等比数列的求和公式是解决本题的关键.

练习册系列答案
相关题目
设△ABC的内角A,B,C所对的边分别为a,b,c,若b2+c2<a2,则△ABC的形状为( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不确定 |
已知双曲线my2-x2=1(m∈R)与椭圆
+x2=1有相同的焦点,则该双曲线的渐近线方程为( )
| y2 |
| 5 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
| D、y=±3x |
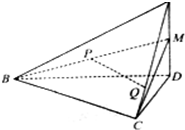 在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,∠DBC=30°,AD=2,BD=2
在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,∠DBC=30°,AD=2,BD=2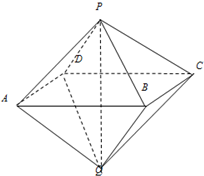 如图,已知两个正四棱锥P-ABCD与Q-ABCD的高都是2,AB=4.
如图,已知两个正四棱锥P-ABCD与Q-ABCD的高都是2,AB=4.  如图,已知△ABC为直角三角形,∠ACB为直角.以AC为直径作半圆O,使半圆O所在平面⊥平面ABC,P为半圆周异于A,C的任意一点.
如图,已知△ABC为直角三角形,∠ACB为直角.以AC为直径作半圆O,使半圆O所在平面⊥平面ABC,P为半圆周异于A,C的任意一点.