题目内容
求和:Sn=1+2x+3x2+…+nxn-1.
考点:数列的求和
专题:等差数列与等比数列
分析:当x=0时,Sn=1;当x=1时,Sn=1+2+3+…+n=
;当x≠1时,Sn=1+2x+3x2+…+nxn-1,利用错位相减求和法求解.
| n(n+1) |
| 2 |
解答:
解:当x=0时,Sn=1;
当x=1时,Sn=1+2+3+…+n=
;
当x≠1,且x≠0时,Sn=1+2x+3x2+…+nxn-1,①
xSn=x+2x2+3x3+…+nxn.②
(1-x)Sn=1+x+x2+x3+…+xn-1-nxn
=
-nxn,
x=0时,上式也成立,
∴Sn=
-
.x≠1.
∴Sn=
.
当x=1时,Sn=1+2+3+…+n=
| n(n+1) |
| 2 |
当x≠1,且x≠0时,Sn=1+2x+3x2+…+nxn-1,①
xSn=x+2x2+3x3+…+nxn.②
(1-x)Sn=1+x+x2+x3+…+xn-1-nxn
=
| 1-xn |
| 1-x |
x=0时,上式也成立,
∴Sn=
| 1-xn |
| (1-x)2 |
| nxn |
| 1-x |
∴Sn=
|
点评:本题考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
一个几何体的三视图及其尺寸,如图所示,则该几何体的侧面积为( )


| A、80 | B、40 | C、48 | D、96 |
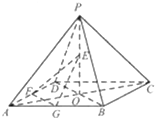 如图,四棱锤P-ABCD的底面为正方形,每题侧棱的长都等于底面的长,AC∩BD=O,E、F、G分别是PO、AD、AB的中点.
如图,四棱锤P-ABCD的底面为正方形,每题侧棱的长都等于底面的长,AC∩BD=O,E、F、G分别是PO、AD、AB的中点.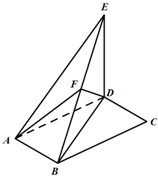 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.