题目内容
设△ABC的内角A，B，C所对的边分别为a，b，c，若b2+c2＜a2，则△ABC的形状为（ ）
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不确定 |
考点：余弦定理
专题：解三角形
分析：利用余弦定理表示出cosA，根据已知不等式判断出cosA小于0，进而得到三角形ABC为钝角三角形．
解答：
解：∵b2+c2＜a2，即b2+c2-a2＜0，
∴cosA=
＜0，即A为钝角，
则△ABC为钝角三角形．
故选：C．
∴cosA=
| b2+c2-a2 |
| 2bc |
则△ABC为钝角三角形．
故选：C．
点评：此题考查了余弦定理，以及余弦函数的性质，熟练掌握余弦定理是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列几个选项，哪个函数是幂函数（ ）
| A、y=x2 | ||
| B、y=2x2 | ||
| C、y=x2+x | ||
D、y=
|
为防止灰太狼的入侵，确保小羊安全，慢羊羊村长对羊村大门设置了“一次一密”的密码保护模式：它使用了四个不同的口令A，B，C，D，但每次只能使用其中的一种，且每次都是从上次未使用的三个口令中等可能地随机选用一种．设第1次使用C口令，那么第6次也使用C口令的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f（x）=
，则f（5）=（ ）
| x+2 |
| x-6 |
| A、-8 | B、-7 | C、-6 | D、-5 |
下列式子中不能表示函数y=f（x）的是（ ）
| A、x=y2+1 | ||
| B、y=2x2+1 | ||
| C、x-2y=6 | ||
D、x=
|
如图，不等式x2-y2-4x-2y+3≥0表示的平面区域是（ ）
A、 |
B、 |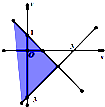
C、 |
D、 |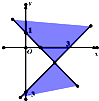
一个几何体的三视图及其尺寸，如图所示，则该几何体的侧面积为（ ）
| A、80 | B、40 | C、48 | D、96 |