题目内容
 如图,已知△ABC为直角三角形,∠ACB为直角.以AC为直径作半圆O,使半圆O所在平面⊥平面ABC,P为半圆周异于A,C的任意一点.
如图,已知△ABC为直角三角形,∠ACB为直角.以AC为直径作半圆O,使半圆O所在平面⊥平面ABC,P为半圆周异于A,C的任意一点.(1)证明:AP⊥平面PBC
(2)若PA=1,AC=BC=2,半圆O的弦PQ∥AC,求平面PAB与平面QCB所成锐二面角的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由圆的性质得AP⊥PC,由∠ACB是直角,得BC⊥AC,从而得到BC⊥平面PAC,由此能证明AP⊥平面PBC.
(2)取AB中点D,PQ中点E,连结OD,OE,以O为原点,OD为x轴,OC为y轴,OE为z轴,建立空间直角坐标系,利用向量法能求出平面PAB与平面QCB所成锐二面角的余弦值.
(2)取AB中点D,PQ中点E,连结OD,OE,以O为原点,OD为x轴,OC为y轴,OE为z轴,建立空间直角坐标系,利用向量法能求出平面PAB与平面QCB所成锐二面角的余弦值.
解答:
(1)证明:∵P为圆周上一点,AC为直径,∴AP⊥PC,
∵∠ACB是直角,∴BC⊥AC,
又BC?平面ABC,半圆O所在平面PAC⊥平面ABC,
平面PAC∩平面ABC=AC,
∴BC⊥平面PAC,
又AP?平面PAC,∴AP⊥BC,
而PC,BC?平面PBC,PC∩BC=C,
∴AP⊥平面PBC.
(2)解:取AB中点D,PQ中点E,连结OD,OE,
∵O,D分别为AC,AB中点,∴OD∥BC,
又根据(1)知BC⊥平面PAC,∴OD⊥平面PAC,
∵半圆O的弦PQ∥AC,
根据垂径定理得OE⊥PQ,∴OE⊥AC,
以O为原点,OD为x轴,OC为y轴,OE为z轴,
建立空间直角坐标系,
∵AC=BC=2,PA=1,
∴O(0,0,0),A(0,-1,0),B(2,1,0),
C(0,1,0),D(1,0,0),P(0,-
,
),Q(0,
,
),
与(1)同理证得AQ⊥平面QBC,
∴
=(0,
,
)是平面QBC的一个法向量,
设平面PAB的一个法向量为
=(x,y,z),则
,
∵
=(2,2,0),
=(0,
,
),
∴
,取z=1,得
=(
,-
,1),
设平面PAB与平面QBC所成锐二面角为α,
则cosα=|cos<
,
>|=|
|=
.
∴平面PAB与平面QCB所成锐二面角的余弦值为
.
∵∠ACB是直角,∴BC⊥AC,

又BC?平面ABC,半圆O所在平面PAC⊥平面ABC,
平面PAC∩平面ABC=AC,
∴BC⊥平面PAC,
又AP?平面PAC,∴AP⊥BC,
而PC,BC?平面PBC,PC∩BC=C,
∴AP⊥平面PBC.
(2)解:取AB中点D,PQ中点E,连结OD,OE,
∵O,D分别为AC,AB中点,∴OD∥BC,
又根据(1)知BC⊥平面PAC,∴OD⊥平面PAC,
∵半圆O的弦PQ∥AC,
根据垂径定理得OE⊥PQ,∴OE⊥AC,
以O为原点,OD为x轴,OC为y轴,OE为z轴,
建立空间直角坐标系,
∵AC=BC=2,PA=1,
∴O(0,0,0),A(0,-1,0),B(2,1,0),
C(0,1,0),D(1,0,0),P(0,-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
与(1)同理证得AQ⊥平面QBC,
∴
| AQ |
| 3 |
| 2 |
| ||
| 2 |
设平面PAB的一个法向量为
| n |
|
∵
| AB |
| AP |
| 1 |
| 2 |
| ||
| 2 |
∴
|
| n |
| 3 |
| 3 |
设平面PAB与平面QBC所成锐二面角为α,
则cosα=|cos<
| AQ |
| n |
-
| ||||||||
|
| ||
| 7 |
∴平面PAB与平面QCB所成锐二面角的余弦值为
| ||
| 7 |
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
如图,不等式x2-y2-4x-2y+3≥0表示的平面区域是( )
A、 |
B、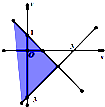 |
C、 |
D、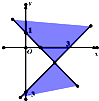 |
若A={x|-1<x<2},B={x|1<x<3},则A∩B=( )
| A、{x|1<x<2} |
| B、{x|-1<x<3} |
| C、{x|1<x<3} |
| D、{x|-1<x<2} |
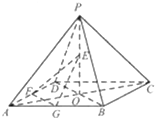 如图,四棱锤P-ABCD的底面为正方形,每题侧棱的长都等于底面的长,AC∩BD=O,E、F、G分别是PO、AD、AB的中点.
如图,四棱锤P-ABCD的底面为正方形,每题侧棱的长都等于底面的长,AC∩BD=O,E、F、G分别是PO、AD、AB的中点.