题目内容
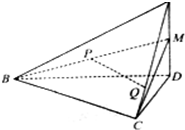 在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,∠DBC=30°,AD=2,BD=2
在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,∠DBC=30°,AD=2,BD=2| 2 |
(Ⅰ)求证:PQ∥平面BCD;
(Ⅱ)求二面角C-BM-D的大小.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)以C为原点,CD、CB、CZ分别为x轴、y轴、z轴,建立空间直角坐标系,利用向量法能证明PQ∥平面BCD.
(Ⅱ)分别求出平面BMC的法向量和平面BMD的法向量,利用向量法能求出二面角C-MN-D的大小.
(Ⅱ)分别求出平面BMC的法向量和平面BMD的法向量,利用向量法能求出二面角C-MN-D的大小.
解答:
(Ⅰ)证明:以C为原点,CD、CB、CZ分别为x轴、y轴、z轴,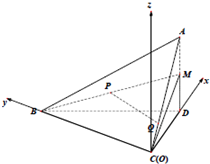
建立空间直角坐标系,
∵在Rt△ABC中,∠BCD=90°,且BD=2
,∴CD=
,CB=
,
则B(0,
,0),D(
,0,0),A(
,0,2),M(
,0,1),
P(
,
,
),Q(
,0,
),
=(-
,-
,0),
平面BCD的法向量
=(0,0,1),
∵
•
=0,∴
⊥
,
∵PQ不包含于平面BCD,
∴PQ∥平面BCD.
(Ⅱ)解:∵
=(0,
,0),
=(
,0,1),
设平面BMC的法向量
=(x,y,z),
则
,
取x=1,得
=(1,0,-
),
=(-
,
,0),
=(0,0,1),
设平面BMD的法向量
=(a,b,c),
则
,
取a=
,得
=(
,
,0),
∴cos<
,
>=
=
,
∴<
,
>=60°,
∴二面角C-MN-D的大小为60°.

建立空间直角坐标系,
∵在Rt△ABC中,∠BCD=90°,且BD=2
| 2 |
| 2 |
| 6 |
则B(0,
| 6 |
| 2 |
| 2 |
| 2 |
P(
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| PQ |
| ||
| 4 |
| ||
| 2 |
平面BCD的法向量
| n |
∵
| PQ |
| n |
| PQ |
| n |
∵PQ不包含于平面BCD,
∴PQ∥平面BCD.
(Ⅱ)解:∵
| CB |
| 6 |
| CM |
| 2 |
设平面BMC的法向量
| n |
则
|
取x=1,得
| n |
| 2 |
| DB |
| 2 |
| 6 |
| DM |
设平面BMD的法向量
| m |
则
|
取a=
| 6 |
| m |
| 6 |
| 2 |
∴cos<
| m |
| n |
| ||||
|
| 1 |
| 2 |
∴<
| m |
| n |
∴二面角C-MN-D的大小为60°.
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
为防止灰太狼的入侵,确保小羊安全,慢羊羊村长对羊村大门设置了“一次一密”的密码保护模式:它使用了四个不同的口令A,B,C,D,但每次只能使用其中的一种,且每次都是从上次未使用的三个口令中等可能地随机选用一种.设第1次使用C口令,那么第6次也使用C口令的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
一个几何体的三视图及其尺寸,如图所示,则该几何体的侧面积为( )


| A、80 | B、40 | C、48 | D、96 |
设Sn是数列{an}的前n项和,且Sn=n2,则{an}是( )
| A、只是等比数列 |
| B、只是等差数列 |
| C、既是等比,又是等差数列 |
| D、既非等比,又非等差数列 |
若A={x|-1<x<2},B={x|1<x<3},则A∩B=( )
| A、{x|1<x<2} |
| B、{x|-1<x<3} |
| C、{x|1<x<3} |
| D、{x|-1<x<2} |