题目内容
已知双曲线my2-x2=1(m∈R)与椭圆
+x2=1有相同的焦点,则该双曲线的渐近线方程为( )
| y2 |
| 5 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
| D、y=±3x |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:确定椭圆、双曲线的焦点坐标,求出m的值,即可求出双曲线的渐近线方程.
解答:
解:椭圆
+x2=1的焦点坐标为(0,±2).
双曲线my2-x2=1(m∈R)的焦点坐标为(0,±
),
∵双曲线my2-x2=1(m∈R)与椭圆
+x2=1有相同的焦点,
∴
=2,∴m=
,
∴双曲线的渐近线方程为y=±
x.
故选:A.
| y2 |
| 5 |
双曲线my2-x2=1(m∈R)的焦点坐标为(0,±
|
∵双曲线my2-x2=1(m∈R)与椭圆
| y2 |
| 5 |
∴
|
| 1 |
| 3 |
∴双曲线的渐近线方程为y=±
| 3 |
故选:A.
点评:本题考查椭圆、双曲线的性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
下列几个选项,哪个函数是幂函数( )
| A、y=x2 | ||
| B、y=2x2 | ||
| C、y=x2+x | ||
D、y=
|
如图,不等式x2-y2-4x-2y+3≥0表示的平面区域是( )
A、 |
B、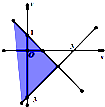 |
C、 |
D、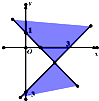 |
一个几何体的三视图及其尺寸,如图所示,则该几何体的侧面积为( )


| A、80 | B、40 | C、48 | D、96 |
数列1,
,
,
,
,
,…,
,
,…,
…的前18项的和( )
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| n |
| 2 |
| n |
| n |
| n |
| A、11 | ||
B、
| ||
C、
| ||
| D、10 |
设Sn是数列{an}的前n项和,且Sn=n2,则{an}是( )
| A、只是等比数列 |
| B、只是等差数列 |
| C、既是等比,又是等差数列 |
| D、既非等比,又非等差数列 |
若A={x|-1<x<2},B={x|1<x<3},则A∩B=( )
| A、{x|1<x<2} |
| B、{x|-1<x<3} |
| C、{x|1<x<3} |
| D、{x|-1<x<2} |
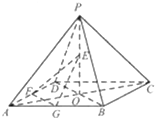 如图,四棱锤P-ABCD的底面为正方形,每题侧棱的长都等于底面的长,AC∩BD=O,E、F、G分别是PO、AD、AB的中点.
如图,四棱锤P-ABCD的底面为正方形,每题侧棱的长都等于底面的长,AC∩BD=O,E、F、G分别是PO、AD、AB的中点.